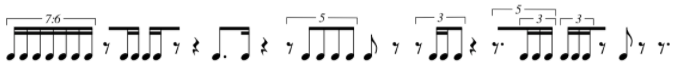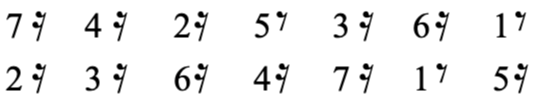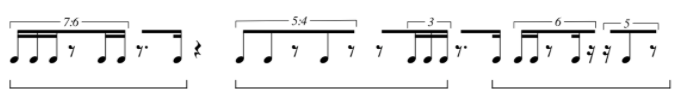Direct Sound

Let's Talk Rhythm Part 3: Rhythm Sieves

3/23/2022

This is a long overdue article that I’ve been getting email requests for since 2015, and it seems like a good time to finally write it. For those of you who have been waiting with bated breath, I hope it lives up to your expectations. As for everyone else, I hope you find this informative and engaging, and as always my inbox is always open for questions.

Enjoy!

Sieves: What are they
Sieves are rhythmic cells and/or longer rhythmic sequences created through basic filtering, mapping, and overlay procedures. They can be simple or quite complex depending on what your goals and working methods are. The concept of sieves is associated primarily with Greek composer/mathematician/architect/awesome dude Iannis Xenakis. My article here is not going to cover the specific processes that Xenakis used because, full disclosure, it’s more complicated math than my brain is able to explain in a simple way (let alone fully understand…), and I’ve found my own idiosyncratic ways to perform similar processes and get quality results. That said, if you’re interested in learning about Xenakis’ rhythmic sieves you can check out Xenakis’ own book Formalized Music (Pendragon Press, 1963…good luck finding this one), James Harley’s Xenakis: His Life In Music (Routledge, 2004) or for the Max/MSP-minded there’s this very nice video.

Rhythm sieves are similar in concept to pitch sieves but different application in order to account for multiple degrees of variation

A pitch range of equally spaced half steps makes filtering a simple process in which all values correspond to number of half steps. It’s a 1:1 process in which half steps are included or excluded from the range

Rhythms deal with different durations, simple and complex beat division, tuplet divisions of beats, interplay of impulses and rests, duration of sustained notes…In short, there’s a lot more to take into account here

Another primary difference is that pitch sieves are a compositional tool to generate a musical structuring element - pitch collections, like a scale that doesn’t simply doesn’t replicate at the octave

Rhythm sieves, however, are a compositional tool to generate fleshed out musical ideas - rhythmic motive - even if simple or not fully developed.

Not to say the results are rigid or fixed by any means
Can be fragmented or used to create germ ideas for more organic restructuring and development

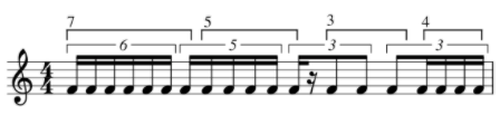
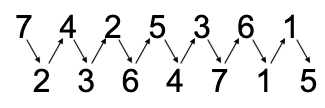
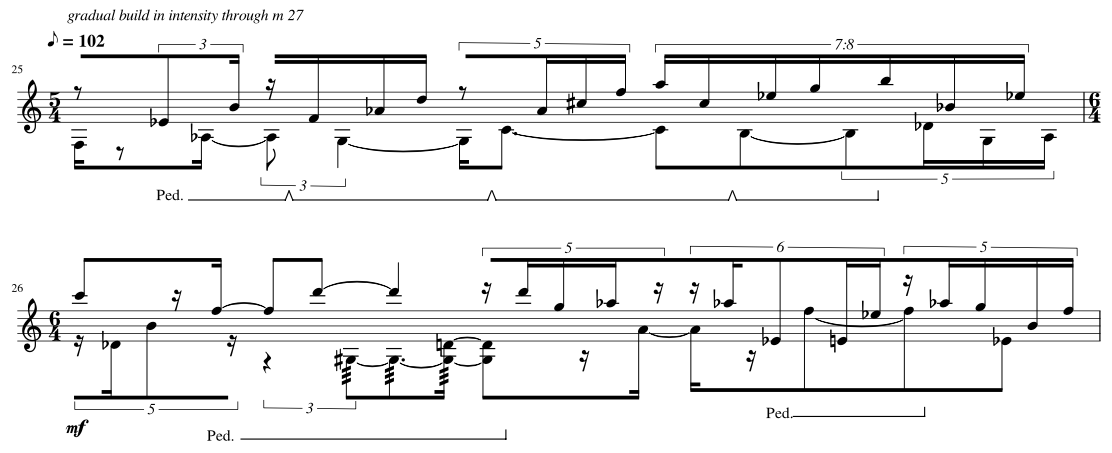
How Are They Created
Again, the information presented below is not how sieves are generated or used in Xenakis’ music, but rather a collection of proportional filtering and mapping techniques I’ve developed and used over the last decade, primarily in the last 5 years. Conceptually they produce the same results as Xenakis, but through different means.

The following are the procedures that I’ve defined

1. Proportion sequence (example 7:5:3:4) mapped directly onto beat structure
2. Proportion sequence mapped with beat/temporal variation among each element and beat
3. Interlaced number sequences representing impulses and rest
a. Interlaced mapped with fixed beat duration
b. Interlaced with variable beat duration
4. Overlaid number sequences representing impulses and rest

Impulse refers to an audible note of undefined duration, and is the term that will be used moving forward.

Proportion Sequence - set of values that have no fixed musical meaning, but are simply values. We’ll use 7:5:3:4 and will map that in various ways.

Sequence Mapped Directly Onto Beat Structure, No Variation (step by step instructions)
Let’s start with the proportion sequence mentioned above - 7:5:3:4. There are two ways to look at this, the first is that a total range is divided into collections of equal subdivisions, such as the example below:

Example 1

This is a fairly basic approach to this filtering process, as it really just consists of stringing together a sequence of numeric values mapped onto a sequence of beat subdivisions. That said, there are a number of ways this could be applied compositionally, as layered streams of repetitive note sequences but misaligned accent patterns. Notice that if you were to repeat the sequence it would begin on the 4th sixteenth note of the fifth beat. This would create a similar effect as we saw in pitch sieves wherein the pattern of half-steps repeats at less than an octave, causing inconsistent pitch collections between octaves. That same approach applied to rhythm results in an accent pattern that does not necessarily repeat on strong downbeats or aligned with overarching metric structure.

This sequence could also be broken by rests to create variation to the pattern:

Example 2

Another approach for mapping the proportion sequence directly onto a beat structure is to simply divide each beat into the specified division.

Example 3

Each beat is divided by the rhythmic value denoted by the element of the sequence - septuplet, quintuplet, triplet, quadruplet. I wouldn’t necessarily consider this a completed sieve, though. This is an example of what I would use for creating an internal shift of energy within a measure of collection of beats - the sequence could also be mapped over a longer period of time - but ultimately this particular example is a building block for a more fleshed out motive. I consider this to be a fairly basic approach to rhythm sieves, but it is a helpful way to break away from standard duple or triple beat divisions.

The second basic method of mapping a proportional sequence is to define a fixed amount of musical time (e.g. a whole note) and then have each element of the sequence take up unequal slices of musical time. This creates internal variation, rendering the actual proportions meaningless, but the result maintains the same division of individual accented impulses. An example of this is shown below using the same 7:5:3:4 collection but the collections of impulses take up different durations of musical time.

Sequence Mapped Directly Onto Beat Structure, Variation Across Beats
The example below uses the same number sequence, but notice the 7 takes up two beats, the 5 takes up a single beat, and 3 and 4 each take up half a beat.

Example 4

Here’s an example of how you can use the same number of audible notes, but the rhythmic values themselves change and cross beats.

Example 5

Notice how each new element in the sequence comes just after each downbeat, similar to Example 2. The beat divisions change on each beat of the measure, similar to Example 3, but the rate of the final element 4 takes up less than a full beat similar to Example 4. This particular example is a combination of all the basic approaches to mapping a proportion sequence (in some cases just a simple integer sequence) onto a collection of beats or range of musical time.

The basic mapping procedures above are conceptually similar to pitch sieves, in that a given range is divided in some way, leaving only portions of the whole. The next collection of methods are more complex and generate more variation than what the basic processes can typically produce. A main difference between the complex sieves and the simple sieves is that complex sieves don’t require a fixed range (or even a defined range at all). They can simply be interlaced or concatenated sequences that go on ad infinitum.

Interlaced Number Sequences for Notes and Rests
The complex sieves take rests into account, not just simple subdivisions of beats. In order to create musical motives we have to take silence and durational variation into account. My approach to this type of sieve is to create two sequences of numbers - these can have repeated values or can be a unique random numbers. One sequence corresponds to audible sound, the impulses.

The first example will combine elements of basic beat mapping, wherein each element of both sequences is a fixed duration, in this case a 16th note. Two sequences are listed below

Impulse Sequence (7, 4, 2, 5, 3, 6,1)
Rest Sequence (2, 3, 6, 4, 7, 1,5)

The first procedure will be interlacing the two sequences starting with the impulse sequence, which creates the following:

Example 6

And when written out as a rhythmic sequence:

Example 7

Each bracketed collection of impulses corresponds to its ordered element in the sequence - the same goes for the rests - but this doesn’t have to be the end of the sequence. Just because the result is shown as a sequence of 16th notes doesn’t mean all rhythmic values have to be the same. This is where creative compositional choices come into play, which we’ll look at further in this article.

From this point you can start to create variation within the sequence by assigning a specific rhythmic value to each element. Here’s an example of what that might look like:

Example 8

In this case the values are defined differently. For the impulses, the rhythmic value represents the fixed duration and the number represents the total number of impulses to be used during that time. The first element would be 7 impulses over the duration of a dotted quarter. Some kind of tuplet would have to be used even if the 7 impulses aren’t the same duration, but the rest that follows has to fit within the preceding tuplet structure. The durations for the rests represent the actual number of that duration. So the first element in the rest sequence refers to two 8th rests. These don’t have to be duple divisions of a strict quarter note, but could instead take up 2 eighths contained in a tuplet.

Here is an example of this interlaced sequence with durational variation

Example 9

At this point the results from these procedures are more musical in nature. Notice in Example 9 many of the impulse groups aren’t all a single duration. This is how you can build additional variation into your sequences. You can take this a step further by adding ties. While that technically alters the number of impulses you still have chunks of durations that fit within the scheme established by the sequence.

Overlaid Number Sequences for Notes and Rests
The final approach to using impulse and rest sequences is to overlay one sequence onto the other. This is similar to the pitch sieve structure where two interval series are applied to a single range.This last approach is harder to deconstruct from the final product, so I’ll break it down step by step. We’ll use the same number sequences as before.

This time rather than have the elements follow one another, each will form a pair consisting of x number of impulses and y number of rests. Given Example 9 above those combined sequences would look like this:

Example 10

In this final method we’ll take these one at a time. In the first pair we have 7 sixteenth impulses and 2 sixteenth rests. My approach here is to place the rests within the collection of impulses. In the event I have more rests than impulses (see element 3 with (2,6)) I typically remove the impulse entirely for a longer rest. There are other rules you could apply, such as defaulting to the larger value and fitting the smaller value inside of it. The example below shows the overlaid sequence above wherein I remove impulses if the rest value is larger

Example 11

Notice the bracketed groupings. They follow a similar energy trajectory and grouping in that they all consist of three events punctuated by rest. Furthermore, the first two contain a block of 1, 2 and 3 impulses, the last containing a grouping of 3 and two instances of 1, but you could take artistic license here and add a second impulse to the last bracketed collection. That would also give you three short phrases of impulses 3-2-1, 2-1-3, and 3-1-2. These could be used as a single extended phrase structure or can be fragmented. Again, these sieves can create complete rhythmic sequences or can be used to generate lots of scraps of rhythmic material to be assembled some other way.

Uses of Rhythm Sieves
In short, I’ve found three primary uses I’ve found in using them in my own music

1. Proportional relationships (same sequence mapped over different durations)
2. Modern take on isorhythm
3. Cohesion without repetition

This section should be regarded as a “how does Jon use rhythm sieves” because the process outlined above has so many possibilities, even when the end result is a fully composed rhythmic motive. As mentioned above, they can be used to generate small rhythmic ideas that can be strung together in various ways, or you could generate a longer rhythm sequence and use it as is. You could resort to thr time-tested techniques for layering rhythms through imitative or invertible counterpoint, even simple rotations or retrogrades can give you a wealth of material to draw from.

In 2019 I wrote two pieces with extensive use of the rhythm sieve procedures outlined above. The first was Mercurial Tendencies II: Marbled Cobalt for solo vibraphone, and the other is Struggling to Breathe for two Disklaviers. In Marbled Cobalt I used simpler sieve procedures to create short rhythm cells, then ordered them in various ways to create a constant push and pull in terms of energy, and used rhythm as a primary source of tension and release. A common theme in the piece is overlaid rhythms that develop over time to become more or less complex depending on the context of the music that comes before and after.

This was my first time using sieves as the exclusive method for generating rhythm. It was very illuminating and presented a challenge I hadn’t come up against in previous works. While I’ve always loved integral serialism of the mid-20th century, I found its approach to serializing rhythm incredibly counter-intuitive. Using sieves allowed me to work within constraints of a system I designed to generate my material, but I wasn’t beholden to the results. Because the sieve procedures are inherently a filtering/mapping process (Xenakis/Ferneyhough) rather than generative (Boulez/Stockhausen/Berio), I feel like I have more control over my material in how it’s applied in mico- and macro-structures of the composition.

Below are two score excerpts from Mercurial Tendencies II: Marbled Cobalt (performed by Tony Donofrio)

Example 12a (click image for audio)

This is an example of two contrapuntal lines. The top line was created using an impulse and rest sequence. The lower line was originally created with an impulse sequence and the rests were added later to fit “inside” the top line. When the two are layered together you can hear the interplay and internal instability that can change quickly (the “mercurial”)

Example 12b (mm. 33-35)

This is an example of the simple procedure of assigning a number of impulses to a beat or collection of subdivisions. Notice that each beat (sometimes two beats or fractions of beats) are divided into a different number of subdivisions. Beats 1-34of m. 33 shows an increase of energy on each beat, but to varying degrees. But beats 5-6 divide 8 sixteenths into 7 - a slowing of energy - while dividing the last 4 impulses into a quintuplet, simultaneously speeding up and slowing down.

In Struggling to Breath I used sieves because of how easy it is to manipulate proportions, and because I knew that Disklaviers would be able to replicate nearly any rhythm I could generate. Over a year had passed since I wrote Marbled Cobalt, and I wanted to approach the sieves with more intention. The central concept/narrative of Struggling to Breathe was inspired by a very nasty lung infection I had in September 2019. The two Disklaviers play almost together throughout the piece, or at least are presenting similar moods and energies. The sieves made it easier to create both short and long rhythmic motives that could be ordered like patchwork between the two instruments.

Below are examples of Struggling to Breathe. You can listen to this piece on my album Galvanized, available on all streaming services.

Example 13a

This is a moment that appears 5 times in the piece, the first instance notated above, the final 2 at a slower tempo and over a longer portion of musical time. It’s a perfect example of using a single rhythm sieve as a means of motivic alteration and development through simple proportional changes.

Disclaimer: I'm aware that 4:3 inside 3:2 in a bar of 2|8 is just 4 16th notes. It's an intentional "mistake" along with a handful of other "mistakes" related to the central concept of the piece. Since it's written for 2 Disklaviers, the "mistakes" are more of a tongue-in-cheek joke rather than serious notation.

Example 13b

This is the final appearance of the motive. Notice the measure of inserted rest (artistic license) and the 6|4 bar that shows different proportions of the same idea. Measure 96 presents the same material without being under the top-level tuplet (3:2 in all) in all 4 voices, effectively slowing the energy and making the layered impulse groupings clearer to identify. There are some liberties taken, but again, artistic license.

If you want to take a deeper look at the score for either of these pieces they can be found on my website (www.jonfielder.com) or you can just click the links below.

Mercurial Tendencies II: Marbled Cobalt (score)

Struggling to Breathe (score) (Apple Music) (Spotify)

Hopefully you found this helpful and gave you some ideas for how to experiment with these procedures in your own music. Remember that sieves aren’t just for creating the angular, dissonant, kerplunkity - devotees, that one is for you - music shown above; but can be used in all kinds of applications relevant to varying styles and aesthetics. Think of sieves as a compositional tool rather than a means to an aesthetic end. I assure you that the sieves will be easier to understand and the possibilities increase dramatically.

Much like other mathematically oriented musical systems, using sieves takes time and practice, and I’ve found the best way to get good results is to dive in and try it. Start small with simple procedures - take fragments and try putting them together by entering rests as you like. Try layering the cells to create a more minimalist driving rhythm. Create short phrases and then make a dozen variations of that phrase using the same basic sieve structure. See if you can create a single sieve (a simpler one is better) that generates a full rhythm motive, then see if you can use that phrase in different stylistic contexts. There are countless applications not bound by style or aesthetic. The only limitations are the ones you, as the composer, place on the system and the artistic implementation of the results.

0 Comments

Defining "Success" In Academia, The Arts, and Music

10/8/2019

1 Comment

Article by guest contributor Andrew Selle

Anyone who even remotely engages with popular culture will be extremely familiar with the trope I am about to describe. You’re watching some mindless television show or move, and a scene takes place in some yuppie-intellectual location that boomers love to hate: a coffee shop, a bookstore, anything with the word “artisanal” in it, etc. The person at the counter looks like they are absolutely hating their very existence, and we come to learn that they went to college for something “useless” like art history, gender studies, or the like. We cut to the sharp, capital-minded main character, and they say something like “Well, that kind of explains it, huh?” Cue laugh track, rinse, repeat. In a very clear way, this cultural trope labels this person working a low-earning job as failed not just because they do not earn much money or have an “exciting” career, but also because they were stupid enough to go to college and study something that so clearly wasn’t going to provide for their financial future.

While we might say that this is just a simple instance of poking fun and that we should have thicker skin (certainly this is a requirement for success in the arts), I would argue that this actually points to a larger cultural problem relating to the way we view the role of academia and the arts in society. Even more, it points to a fundamental issue with the ways in which society attributes value, namely, that it often correlates a pursuit’s value with its capacity to generate wealth or power. In a capitalist society, this should come as no surprise; however, this creates an obvious discontinuity between said society and academic/artistic pursuits: if pursuits which have a high potential for wealth creation are positively valenced from a cultural-capital standpoint, the opposite must be true of those pursuits that do not inherently create wealth. Herein lies the problem.

This problem first presented itself to me a number of years ago as I was reading an editorial in the Wall Street Journal by Douglas Belkin entitled “Many Colleges Fail in Teaching how to Think.” In his article, Belkin rightly asserts that students are often spending 4+ years in college but not coming out with many more critical thinking skills than they enter with. Those of us that have been around academic for any amount of time know this all too well. Unfortunately, he is far too quick to pin this on the universities themselves (evidenced by his title saying the colleges themselves fail). What he misses is that universities have been so culturally pressured to become vocational institutions rather than institutions of higher learning, such that the critical thinking skills he is referring to have no place in the curriculum anymore. Modern culture has become so preoccupied with the university degree as a route to monetary success, and universities have responded to that pressure.

After reading this, I was so incensed that I quickly began typing up a letter to the editor. While I will not recount my entire tirade here, one bit of research that I did sticks out. In his 1873 text The Role of the University, John Henry Newman addresses this issue. He says, “If then a practical end must be assigned to a University course, I say it is that of training good members of society…” Herein lies the value of a university education; it lies in broadening one’s horizons, coming into contact with people and ideas that are foreign to you, and the pursuit of learning and critical thinking for their own sake. The value in a university education is distinctly not monetary; the institution of the university itself was never designed with this in mind. Thus, we arrive at the tension between the intrinsic nature of the university (the pursuit of education) and the cultural shift in the view of the university (as vocational preparation and wealth creation).

So, where does this leave the arts? I think there are two very clear ramifications for the arts that result from this sort of societal and cultural pressure. One is obvious, the other, less so. First, and most obviously, in a cultural context that positively values those pursuits that generate wealth and/or power, the arts is in a bit of a bind in that it typically is not a huge generator for either. (Yes, artists that make it really big tend to make a lot of money, but the proportion of artists that make an above average salary compared to, say, accountants or lawyers is certainly smaller.) Thus, arts programs at all levels of education have to find ways to justify their existence in the absence of a realistic potential to be lucrative. We hear these tropes all the time: “Arts make the world worth living in,” “Kids who are involved in the arts to better in school,” and most nefarious of all, “Highly creative people are highly employable people.” (These are just a few of the many.) In this way, arts programs have to define their value and their success not on intrinsic factors like personal fulfillment and creative experience, but rather as a utility to external forces such as employability and performance in other facets of modern life deemed more “useful.”

There is, however, a second, less obvious issue that arises when we determine value in this manner. Not only do the arts themselves need to justify their own existence, but I have found that artists themselves split into sects and infight over whose pursuits are more marketable. I was very fortunate to attend a university for my two composition degrees that never really concerned itself with the amount of money that a student’s work might generate. Never once did I hear someone say “Well, that’s an interesting idea, but no one is going to buy it.” However, we all know that this is not the case everywhere. Every day, students’ artistic pursuits across the country are guided by speculation of future success as measured by marketability and not creativity. Of course, I can certainly forgive an institution for pushing their students toward more marketable forms of artistic expression when the institution’s very livelihood (and that of the department) rests on their students becoming successful in terms of the culture that surrounds it. It is all too easy to point the finger at the institutions, but the finger should really be pointed at contemporary culture, and ultimately, ourselves. That, out of all of this, might be the toughest pill to swallow. We all, in some way or another, are complicit in this modern system of “university as vocational training.”

This is where the crux of the issue lies: with us. I am guilty of this, without question. For years, I justified my pursuits of experimental and contemporary music by saying things like, “Well, you’d be surprised how much money you can actually make doing it,” or, “I know it’s not the most lucrative career field itself, but I’m definitely learning skills that could get me into something a little bit more secure,” etc. I’m sure you’ve all said something similar; as ashamed as I am, culture is one hell of a drug. However, here is my plea: no more. No more should we have to justify our pursuits by anything other than their intrinsic value. Toward the end of my doctorate, I was often getting the question, “Huh, so music theory…what are you going to do with that?” It took me a while, but I finally started answering, “What do you mean? I’m doing it now.” Those were some of the most empowering words I ever said, and still feel so to this day.

To those of you in academia, the arts, culture studies, or any sort of related field that contemporary culture hasn’t sanctified as “valuable,” I would encourage you to define your success in the self-fulfillment of the pursuit itself. Do not feel pressured to justify your actions in terms of some future or tangential monetary or cultural gain. At the heart of it all, there is honor and value in the pursuit of learning and creative expression of any kind. If you wake up and get excited about the art you make, the words you write, the things you read and study, and the thoughts and feelings that these pursuits stir within you, you are successful.

Ultimately, it is up to the university itself (and those of us involved in academia) to try to reorient the cultural milieu around the institution. We should advocate for these pursuits not because our students will earn high-paying jobs (though they might) or because they will be ensconced into positions of power and import, but because these pursuits are an inherent part of being a good citizen. To return to Mr. Belkin’s editorial, we need to remove the vocational aspect of the university and teach our students and each other to be critically-minded individuals. That, and not the potential to amass wealth, should be the cultural marker of success. In other words, is it the art-historian barista who has found intellectual fulfillment that is the failure, or is it the expression-starved culture that needs to be reassured that they are fulfilled?

Dr. Andrew Selle is a music theorist and composer and is currently a lecturer in music theory at Purdue University Fort Wayne.

1 Comment

Yours, Mine...Not Necessarily Ours

8/8/2019

0 Comments

In true Nietzshean fashion I am here to proclaim The Audience Is Dead...or at the very least it does not exist. Obviously this is a bit dramatic, but not entirely untrue. I decided to write this post after reading a recent article run by RTE (Ireland’s National Television and Broadcast media outlet) titled “Is Experimental Music Killing Classical Music?” by Dave Flynn. The following is not specifically in reference to Flynn’s article (which for the record I find to be unbelievable off-base), but more in response to the many discussions that ensued in online forums and across social media. A conversation I often found myself in with other composers, performers, theorists, musicologists and even casual listeners of contemporary music focused on whether or not Flynn is right in reference to writing music “for the audience,” and the general “accessibility” of said music. I have always found both of those sentiments frustrating for a number of reasons, all of which I will discuss (and vent about) below.

Before getting into any kind of nuanced discussion of why the concept of writing for “the audience” is problematic I would like to revisit my opening statement - the audience does not exist. This might seem a grandiose and even polemical statement of Boulezian proportions (not that there’s anything wrong with that), but there is a great deal of truth to it. The problem is not the idea of audience, but with the definite article used to describe the noun. It would be easy to refer to “an” audience of listeners, but “the” carries an implication of a definable audience. On the one hand this could be ignored as a nit-picky prescriptivist complaint, but I don’t see it that way. Differentiating between definite and indefinite articles is a key element here because “an” audience could denote any group of people encompassing a wide range of ideas, cultures, aesthetics, approaches, and values. However, “the” audience implies a single monolithic group of shared ideas, cultures, aesthetics, values, and, above all, shared expectations.

To me it goes without saying (even though I already said it) that in order to different levels of specificity in any capacity one can easily do that through the use of definite and indefinite articles. I could say the sentence “please go get me a soda” implying that any hypothetical soda will adequately quench my thirst. However, if I were to say “please go get me the soda” that then implies I’m asking for a specific type of soda. Again, this is all straight-forward. However, this concept is often not applied when discussing art and music, specifically when discussing contemporary concert music. I find that lack of distinction quite disconcerting, though, because of the implications and restrictions it places on artists, as well as listeners.

My soda example might not be the best analog to the situation of discerning between audiences, mainly because with the soda the idea is that a single person is drawing from a wide range of possible choices or from a single specified choice. When composers and performers write and program music they are creating a single entity (the piece of the concert program) that is meant to satisfy, entertain or engage a wide collection of people with varying ideas and sensibilities; the input/output is reversed so the paradigm must shift. There is quite literally no way to refer to any listening body as “the” audience in relation to aesthetic tastes and sensibilities. If you were to say “the audience will leave immediately following the last piece” well then that definite article is entirely necessary. However, the phrase “I wrote this piece with the audience in consideration” is immediately rendered meaningless because there is no way to define what “the audience” is, or who it encompasses. There is no single group of listeners/appreciators that all artists can or even should strive to please. The audience for one avenue of art could be the polar opposite of the audience that is attracted to a different type of art. To try to please both is an exercise in futility. An audience of listeners who responds positively to Post-Minimalism could potentially (and likely) have the opposite reaction to New Complexity. Does that mean that a Post-Minimalist is writing for the audience and the New Complexity composer is not? That would be a hard no. Each is writing for their own audience of listeners with a general set of expectations in mind.

This leads me to my next point, which is how and why the concept of “the audience” is damaging to composers, performers, and even to any listener of any type of music. This goes back to my point above that the concept of “the” audience is a reductive concept that lumps all listeners and appreciators of art into a single category wherein its members have shared interests and expectations. How could any composer write music to please such an audience? How could a performer craft a program to engage the entire audience? Above all, as an audience member I would be a bit offended (for a fleeting moment) if a composer with diametrically opposed aesthetics told me that they were writing music for “the” audience, because they are clearly not taking my interests and tastes into account. On the same token, as a member of “the” hypothetical audience of shared interests, that audience is not taking into account the vast number of voices and styles that are available. There are a myriad of reasons that listeners might latch onto this viewpoint, specifically in the interest of maintaining what certain members might deem universal interests. However, those interests are destined in any situation to remain murky and undefined. The artist cannot expect to please everyone. The audience cannot expect to establish a single set of expectations to which the creator and curator must adhere.

Furthermore, writing to the tastes of “the” audience also implies that there is a limited amount of musical material, complexity, variation and experimentation that listeners are willing to and/or capable of digesting. This simply isn’t true. As a composer of what some might deem “challenging” music, I have found that my highest compliments have come from non-musicians and from audience members who did not know what to expect from my music. In fact, in some cases where my music was an aesthetic outlier on a program, it was the lack of adhering to expectations that drew listeners in and gave them some level of pleasure in hearing my work. Does this mean you as a composer, performer or concert curator should have no consideration of who is listening to the music and what a specific group of listeners with shared interests will like? Absolutely not.

All genres and styles of music have an audience to some degree, and those audiences generally want to hear what they like, not what a hypothetical body of tastemakers has approved. It’s important to know which musical elements and components make up a certain style that appeals to any given audience, but it is my personal belief that compositional decisions should not teeter on the opinions and sensibilities of an undefined group of listeners. For me, it is important to know who is primarily listening to my music, but I don’t always approach composing pieces in the same way, nor do I expect the same group of people to enjoy all of my music. Some pieces will appeal to one group of people while simultaneously boring or even irritating another. Above all, it is the duty of a composer and performer to create art, and it is the duty of listeners to seek out the music they enjoy. At the risk of possibly offending some readers, it is not my job to cater to your tastes.

My final point in relation to this topic is that referring to any rigid idea of what “the” audience is really only establishes aesthetic battlegrounds and in-fighting among artists and creative minds. Composer A writes for “the audience” whereas Composer B does not, or at least not overtly. In some circles of New Music, Composer A might be seen as a paragon of contemporary music, bridging the gap between esoteric modern music and “the” audience who doesn’t want to stray far from the tried and true chestnuts of the canon. Composer B might be creating art that they truly believe in and which is creative, colorful, engaging and thought-provoking...if only they had considered “the” audience. But who determines which composer writes for “the audience” and what metrics are used to determine that? Obviously there is no answer to that question if you agree with any of what I have said above, because if the premise of the existence of “the audience” is untrue then why bother trying to determine the characteristics that define said audience.

Additionally, Writing for the audience is a dog whistle term with a subtext that implies music for “the” audience is accessible, digestible, and worthy of praise or at the very least of multiple performances. This kind of idea has been used for decades to deride the art of experimental musicians (composers and performers) and of atonal, spectral, electroacoustic and all musics not deemed accessible enough. This was a constant point of discussion when I was in graduate and doctoral school, and would inevitably lead to some of the most heated and contentious discussions during composition seminars and among friends over drinks. So often I found myself explaining to friends and colleagues “I am writing for the audience...just not yours. You are writing for the audience too...just not mine.” It should be mentioned that this perceived accessibility is often (at least in my experience) viewed through the lens of orchestral programming which is historically ultra-conservative, further pointing to the dog whistle tactic of disparaging the experimental music that Flynn’s article claims is killing the canon, and Classical music altogether.

In summation, it is my overall goal that we as a community of New Music makers abandon this preposterous idea of the existence of “the” audience. It really doesn’t even make sense from a linguistic standpoint - a definite article implies a definable noun or entity, which is impossible when considering subjective taste - and it definitely makes absolutely no sense from a creative or application standpoint. The concept of “the audience” rejects outside ideas, condemns experimentation and limits prospects for growth and change within an art form by limiting creativity to some imagined rubric of ideas, aesthetics and sound worlds. Beyond that, a perceived lack of audience consideration is used to level criticism against composers and performers, and to justify the exclusion of their music and art. It’s my hope that we can start to move away from this damaging and unattainable goal, and perhaps focus more on writing and programming music geared toward your own audience, whatever and whoever that might be, with the goal of simultaneously trying to reach listeners outside of your own. If you’re successful in doing that, please tell me how. In the meantime, create what you love, perform what you love, and those with shared interests will appreciate it. Those without will surely find something that appeals to them as well.

0 Comments

Music and Mental Health: Complementary, Not Contradictory

7/26/2019

0 Comments

BY JON FIELDER
MUSIC AND MENTAL HEALTH: HOW DIAGNOSING/TREATING MY MENTAL ILLNESS SAVED MY CREATIVITY

The role of mental health on creative individuals is not a new topic, and while there is a stigma surrounding mental health in America, it seems almost a romanticized component of artistic impulses and creative output. From the giants of art/music history such as Van Gogh, Poe, and Beethoven to modern examples like Antonin Arteaud, Jaco Pastorius, Syd Barrett, Mariah Carey, and Kanye West you can easily find links to creative people who live with mental health issues. I can add myself to that category of creative minds (related only by mental health, not by prestige). My battle with mental illness is more recent in my adult life, but it has nonetheless had a profound impact on me, both personally and creatively. Before continuing with any discussion of how understanding my mental health impacted my music, I would like to tell my story of how I got to where I am today. While the following is ostensibly long-winded, I feel the level of detail is necessary to understand just where I was mentally and emotionally leading up to my diagnosis, and how my behavior not only impacted me and my creative output, but also my fiancé (now wife) Michelle, and the critical role she played in helping me get better.

In November of 2017 I was diagnosed with Bipolar II disorder. This came after a long period of battling symptoms of depression and a dearth of creative output. Upon finishing my doctoral studies at the University of Texas at Austin I moved to the San Francisco Bay Area to live with my fiancé, Michelle, and start a new life together. Following the completion of my dissertation (double-bar in February, defended in April) I experienced extreme difficulty in focusing on achieving any compositional goals, and a dramatic rise in anxiety and general frustration with the world around me. At the time I chalked it up to the stress of moving, difficulty in finding employment, adjusting to living with Michelle, which we had not done in the previous years we had been together (long distance for nearly two years). My erratic behavior and shifts in mood seemed like byproducts of my environment and the extreme changes to my life, which had been wrapped up in the university system for 12 years. I didn’t really know how to exist outside of that world and I found the adjustment difficult to navigate, as I expect anyone would. The stress and anxiety felt normal, and in all honesty were not new to me. I had similar experiences when transitioning from undergrad to grad school in 2010, and a slightly less intense version when I moved to Austin in 2013.

Still, while these feelings weren’t without precedent, at the time I lacked the introspection and self-awareness to realize that what I was experiencing was not typical behavior. While it may have been normal for me, it was not characteristic of a mentally stable individual. Though I found a teaching job in July - only two months after making the move - it was an adjunct position and wasn’t as fulfilling as I had hoped for. I refused to seek out new friends, I stayed in my apartment on days I didn’t have to work, and I made no attempt to explore my new city, which is arguably one of the coolest places in the United States. Most importantly, at least to me at the time, was my complete inability to write music. It wasn’t the first time in my life I had gone through a compositional dry spell, but it was the first time that I felt completely incapable of writing music. I would stare at notebooks and staff paper for hours and come up with nothing. It would have been one thing if I had scribbled some ideas and later tossed them out because they weren’t what I was looking for, but I wasn’t even able to do that. I sought out a new therapist to talk about these personal issues, as well as the growing problems with communication I was experiencing with Michelle.

To say that I was difficult to be around and live with would be an understatement. I was angry, unmotivated, anxious and on edge all the time. I never wanted to do anything or go anywhere on my own, but I was also angry that I felt cooped up in our tiny apartment looking at blank pages staves for hours on end. I took everything as criticism and I compared myself to my friends and colleagues who I felt were doing better than me professionally and personally. I didn’t understand why my many years of academic training and teaching weren’t enough to help me find gainful employment as a teacher. Moreover, the years I had dedicated to honing my craft seemed pointless at this stage in my life since I couldn’t even come up with even one basic germ of an idea for a new piece. It was as if I needed the structure and deadlines of the university system to create.

I felt trapped, isolated, confused, and angry. And I took these frustrations out on Michelle with staggering regularity from May through November. It was exhausting for both of us, and even with weekly therapy there seemed to be no improvement and, at least for me, there seemed to be no end in sight.

After six months of what seemed like an endless cycle of personal frustrations and failed attempts to get my life together (what I felt was of no fault of my own), the fighting had reached a breaking point on Thanksgiving Day. I wish I could say I remember the details of that day vividly, but unfortunately one of the effects of my Bipolar II is that during moments of extremely heightened anger or mania I tend to black out portions of my day. All I remember is having a very intense shouting argument with Michelle. After taking an Ativan to help calm my nerves enough to talk I was still going full force. It even got to a point that I was literally falling asleep - a side effect of the benzo - and I continued to mumble angry retorts through dozing off. Michelle told me that something was wrong, that this wasn’t like me. She begged and pleaded for me to go to the hospital, because nothing seemed to help. So I listened to her and I immediately went to the local Kaiser Permanente hospital and checked myself in. I was there for about 2 hours, spoke with an on-call psychiatrist who wrote me a script for Zoloft and scheduled an appointment with me two weeks out. They said I might have Intermittent Rage Disorder and told me to try to just remain calm and relaxed while at home or at work. I went home with the Zoloft in hand, hoping it would help.

The next morning Michelle and I woke up and within 10 minutes we were back to arguing about the previous day and night. At this point I absolutely snapped. I told her I was leaving, packed an overnight bag and left. After walking around the town for a few hours I eventually went back to the apartment. When I got back Michelle pleaded with me, again, to go back to the hospital. Something was clearly wrong, and I needed some kind of attention from a mental health professional. I went back to the hospital, was kept overnight and the following morning I met with a psychiatrist who diagnosed me with Bipolar II and discussed my options for immediate treatment. The next few months (December through mid-January) were a difficult transition, but the full dose of medication eventually took hold and I started to see some major changes. I handled stress and anger better, my communication started to improve, and I noticed small changes in my overall behavior. What I previously identified as anger and stress I could now identify as mania (or hypomania, more specifically). Periods of lethargy wasn’t just laziness; I was cycling into depression. I now had an understanding of what was happening in my head, and I knew how I could manage it, and work with it to make the best of my life and circumstances. I felt better equipped to navigate the world around me with my new found grasp of how my mental processes operate. I don’t see my mental illness as a hindrance, but as something I just need to be cognizant of, and know how to identify warning signs of cycling behavior patterns.

That leads us back to the beginning - how an understanding of my mental health saved me creatively. The prolonged dry spell ended very quickly after I started taking medication. My first dose of Lamictal was taken the morning after I left the hospital on November 25. By the last week of December (still not at a full dose yet) I had started working on a new piece for bass clarinet and live electronics. I didn’t have high hopes, as I had started working on that piece earlier in the year after moving to California (around late May) and gave up after only a 3-4 weeks of failed attempts to even get some basic sketches done. This time around was different, though. I was able to create the kinds of sketches I was used to making. I had ideas for rhythmic patterns and ways I could create variations for the melodies. I could hear the electronics in my head and was already planning the live processing and structure of the Max patch. It was coming together more quickly than anticipated.

By mid-January 2018 I was finished with Broken Earth/Crags Ascending for bass clarinet and live electronics. Was it my best work? Not at all. But I hadn’t felt a sense of pride and accomplishment since I completed Dissociation Sequences (my “greatest hit” to date) in fall of 2015. I was hesitant to get overly excited, though. It was likely that this was just a fluke, a brief outpouring of creativity that was sure to run out. But it didn’t. I got hired for a full-time teaching position in January and had my own wedding to plan, so I took a break from actively composing until after the wedding - it was now late January and the ceremony was in April, so I had a lot on my plate. I continued to sketch little ideas, though. I kept two small notebooks with me all the time - one of staff paper, one with blank pages - and would jot down fragments of ideas on the train and bus to and from work. I wrote short descriptions of ideas down during my lunch breaks. I would make charts if pitch set relations and work out pitch sieves in my free time. I was building a collection of building blocks for when I was able to get back to writing.

After the wedding I got back to work, and 2018 proved to be one of my most productive years to date in terms of sheer output and quality. During the break from January to April I took some time to also work on an EDM album I had in the works for years and never had a chance to finish. This resulted in completing a 7-track album (Gnarlyshkeit), all finished in just under 3 months. Immediately following Gnarlyshkeit I started working on a piece for electric guitar I had put on the back-burner in 2015 and never came back to. I completed it in a little over 4 weeks, the result being Mercurial Tendencies I - Dyschronometria. While I was in the editing stage of Dyschronometria I started sketches on a piece for speaking percussionist and djembe - another work I had planned on doing for years and never got around to it. That eventually became He Gnashed In Fury, completed in September of 2018. I then immediately started a piece for solo vibraphone - Mercurial Tendencies II - Marbled Cobalt - and finished it in late November. I concurrently started working on a piece for cello and live electronics - an elegy to my friend and mentor Ed Pearsall, who passed away the evening of my second hospitalization. That piece was completed in the first week of December. I then moved on to two trios - one for flute, cello and piano (Mercurial Tendencies III - Paroxysm), the other for flute, oboe and Bb clarinet (Seeking the Edge of Chaos).

All in all, I completed a total of 5 very dense solo pieces - 2 with live electronics - totaling just over 30 minutes of music, started (and nearly finished) two trios, wrote/recorded/produced a 30-minute EDM album, all while working full time and getting married in the middle of it. For a period of time I attributed this uptick of compositional accomplishment as the end of a compositional dry spell, and the result of a much needed break from composing following the completion of my dissertation. But when taking into account what seemed like a complete inability to create for the majority of 2017, which was preceded by a dearth of output from mid-2016 through the completion of my dissertation, I cannot underplay the key role that diagnosing and treating my mental illness played in this process. I have Michelle to thank for that. I would likely have not sought any help on my own, and it’s hard to tell how my life would have played out as a result.

Furthermore, I noticed a drastic change in the music I was creating. I shifted my focus from pitch and timbre to rhythm and gesture. I started experimenting more with various methods for controlling temporal relationships, utilizing more complexity of rhythmic notation through nested tuplets, irrational meter and metric modulation. I had employed these compositional techniques in previous pieces, but not to the degree that I did in my pieces from 2018, and definitely not with the rigor and understanding of my more recent compositions. Upon further reflection a common thread began to emerge. My methods were not simply controlling temporal relationships, but were always creating a dichotomy of stasis and turbulence, of placid reflection articulated by violent outbursts of energy. While it was not done intentionally, I could see myself engaging with my current worldview colored by a new found understanding of my own mental processes. The constant turmoil of my life in previous years of undiagnosed and untreated mental illness had manifested itself in my creative impulses following the diagnosis and treatment. I sought control over my materials, and I now knew how to achieve that control. I also developed a better understanding of how to work with my materials to gain the complex relationships of time, rhythm and gestural shaping that could convey the sounds in my head, the music I wanted to create.

There is also a kind of struggle that goes into preparing and performing these works. This is not lost on me, but the difficulty in securing numerous repeat performances is not a deterrent. I realize that the music I’ve been writing since ~2010 is very difficult to play, and that it has only increased in difficulty in recent years (this is why I tend to only work with performers who want to play the kind of music I write). That said, I feel that my output demonstrates a command of materials and an intentionality of sonic results that I haven’t been able to attain in previous compositions. My hope is that a performer who would choose to perform one of these works (and potentially subsequent ones) would bring an element of the struggle and effort that went into rehearsing and preparing the work into the live performance. I write these pieces, in all of their notational density and complexity of time, with an understanding that they will never truly be performed with mathematical accuracy, but that isn’t the point (this is another conversation for another time). The point is that the performer capture the essence of the piece with as faithful a replication of the score as they can. In a way, an attempt to perform one of these pieces is an extension of what I outlined above - a desire and attempt to control something that in reality is ultimately out of my hands. I can keep my Bipolar cycling under control for the most part through medication and self-care, but I’ll never truly be able to keep it from affecting my life. In the same way, I can manage every minute detail of my music and notate what would be an “ideal” representation of my thought processes, but the reproduction of that is up to the performer, and I will gladly relinquish that final authority to someone more capable than myself of realizing my creative processes filtered through a newfound understanding of my mental processes and my unending efforts to engage with them in a healthy and meaningful way.

The final point I want to touch on related to mental health and artistry relates to a recent episode of David Letterman’s “My Next Guest Needs No Introduction,” in which he interviewed Kanye West. It has recently become public knowledge that Kanye was diagnosed with Bipolar I (different from my Bipolar II diagnosis; behavioral trends are similar, with differences severity and rate of cycling). Some celebrities and individuals came out in support of Kanye’s discussion of his mental health, noting that it was important that a celebrity with so much influence was so open about such a personal and stigmatized topic. But that openness about his experience is exactly what I found troubling about Kanye’s interview. He was very up front about his own mental processes that occur during a manic state (what he refers to as “ramping up”) and the erratic behavior and potential hospitalization that can come from that. I think it was important for people who are unfamiliar with Bipolar disorder, and mental health in general, hear a celebrity with Kanye-level fame talk so candidly.

However, I did find his interview very troubling when he started to talk about his treatment. He told Letterman that he was using “alternative treatment methods” overseen by a doctor to help with his disorder. He did, however, say that medication *might* work for some bipolar patients. This is what I found so problematic, and what I continue to find infuriating about many celebrities in their discussions of their struggles with mental health. Kanye has consistently spoken out against medicating himself to treat his Bipolar disorder, and as a person with heavy influence over a number of people that can influence how Kanye’s fans feel about mental health. West’s outspoken attitude against medicating mental health diagnoses is so prevalent that Pete Davidson made a joke about it on SNL’s Weekend Update, the punchline being “Take ‘em [meds]. There’s no shame in the medicine game!” I found Pete Davidson’s approach to the topic much more uplifting than Kanye’s. Mental health is stigmatized enough, and patients are already incredibly hesitant to even start a medication regimen, let alone stay on one. When a highly regarded celebrity like Kanye West comes out and openly talks about having a mental illness that is a big step forward. When that same celebrity then talks about they refuse standard medical treatment and medication that is taking huge steps back. It might raise awareness of the presence of mental health, but it further stigmatizes the use of medication as treatment. Therapy is incredibly helpful, finding a support system is helpful, maintaining a healthy diet and exercise routine is helpful, talking openly and accepting your mental illness is helpful ...refusing to take medication because you’re worried it will ruin your creativity is not only short-sighted and misguided, it is legitimately dangerous. While some might applaud Kanye for his candor, I’m afraid all I can do is sit back, shake my head and do my best to help inform people through my own experiences and struggles. And for what it’s worth, I agree with Pete Davidson on the meds...take em!

_________________________
Thank you for taking the time to read this post. If you are experiencing any struggles in your daily life, I strongly urge you to seek out help. There is no shame in needing help with mental health, and there are resources out there for support. Mental health treatment is not a one-size-fits-all solution, and just because my transition was relatively fast and effective, not to mention beneficial to my creative output, does not mean it will be that way for everyone. However, I cannot stress enough the importance that mental health care has had on my life and on my loved ones. Please reach out to one of the numbers below if you feel you are in a mental health crisis or need to speak with someone. My inbox is always open if you ever want to reach out.

Suicide Prevention and Crisis Hotline: 1-800-273-8255
National Alliance on Mental Illness Hotline: 1-800-950-6264
Substance Abuse and Mental Health Services (SAMHS) Helpline: 1-800-662-4357
SAMHS Disaster Stress Helpline: 1-800-985-5990

0 Comments

Some Thoughts on Musical Inherence, Structure, and Aesthetics

1/3/2018

0 Comments

by Andrew Selle (guest writer)

(Footnotes at end of post)

Each of us has our own innate beliefs and intuitions about what music “is,” if it can be anything. To some, only the high Classical really counts, and the flowery, indulgent ornamentation of the Baroque and Romantic styles are simply too much. (This is to say nothing of the common response to Modernist and contemporary music.) To many others, the concept of “music” can be defined much more broadly, and many sounds, even those that are traditionally “non-musical” might be included in this wide scope of musical appreciation. However, this discussion is not about what music is; even if I felt I had an answer to this question, it is perhaps a fool’s errand to try to convince anyone what music may or may not be. Instead, what I wish to discuss is the various ways that we talk about music and the properties that we impose upon it, especially in terms of musical structure. By “structure,” I do not simply mean form (although form is undoubtedly a part of it); rather, I mean the perception of the construction and deployment of an entire musical work or series of works, including musical discourse, syntax, form, and even potential semiotic units.
My central argument about musical structure is simply this: music cannot have structure. The careful reader will note that I did not say listeners are unable to perceive structure; this is surely not the case. (Else an enormous part of the music-theoretical world will surely be cleaved, and an entire generation of theorists might be ridiculed.) Listeners can undoubtedly perceive musical structure, but it is often the case that we are too quick to attribute this perception to a property that the music “has” rather than as a construct that we impose upon it. To put it simply, if music has structure, it is because we, the listener, need/want it to. The invocation of musical structure relies entirely upon the listener and his or her extra-musical knowledge and experience; the music itself is nothing more than different frequencies at various energies over time, nothing more, nothing less. To use an analogy, imagine the Mona Lisa, one of the most (or perhaps the most) famous paintings in the world. When we look at this painting, we see the structure of the work immediately: the fair woman in the foreground of the painting with a sort of half smile set against a landscape behind her. Now, imagine this image being viewed by a life form who has never seen a human being nor any other type of humanoid creature. What would it see? Surely, it would not see or comprehend the same things that we do when we look at the painting, but rather it might see a series of colorful splotches and lines. It would be able to describe the painting in terms of concepts that it understands, but this description would scarcely overlap with our own. Our experience tells us that this painting is of a human because we understand the concept of the human “structure.” Similarly, when we talk about a musical structure, we must speak in terms of our own experiences. Thus, when we say that a particular piece is in “sonata form,” for instance, we are imposing this structure on the work; it is not a property that the music inherently has.1 As I stated above, if music has a structure, it is because the listener or analyst perceives it through extra-musical experience, not because the music has it.
What is the point of making this distinction, though? On the surface, this is an innocuous debate at best, and a pedantic philosophical slog at the worst. The problem is that time and again, theorists and critics make aesthetic and qualitative judgments about music, especially new music, based on the premise that it can have structural properties in the first place. In lieu of stating a simple distaste or unfamiliarity with contemporary and experimental music, conservative critics pass the buck onto the music itself for failing to pass some sort of a priori aesthetic or structural examination. Consider the following quote from Wallace Berry: “little if anything is more vital in musical form than the controlled maintenance, and effective change, subsidence, and direction of motion. Failure to move with conviction and direction is one of the most common and crippling defects of ineffective music.” He goes on to conclude that, “Without order, the musical material, however sound and vigorous, may be reduced through its aimless diffusion to an impotent stammer whose impression dissolves as it is issued, lacking the exercise of whatever potential may exist in it for assimilable unity, and renouncing all possibility of intellectual appeal.”2 It is not difficult to figure out what music it is that Berry considers “ineffective.”
This sort of aesthetic judgment based upon the idea that “Music” inherently has certain structural qualities allows for a not-so-subtle reinforcing of the traditional musical canon. It sets up an a priori aesthetic strawman against music that one does not like, and then the critic is allowed to pass it off as objective observation rather than subjective preference. “See, it’s not that I don’t like this music; it simply doesn’t have the inherent qualities that turns sound into music!” This type of logic should sound very familiar to anyone who has studied the theories and writing of Heinrich Schenker, perhaps the most influential and controversial figure in modern music-theoretical history. To put it as simply as I can for the uninitiated, Schenker theorized that all musical works can be understood as a linear prolongation of the tonic triad, consisting of a bass arpeggiation between I and V and a fundamental melodic line from scale degree 3 to 1 (and sometimes 5 to 1 or rarely 8 to 1) filled in with passing tones.3 It is not hard to quickly come up with a list of musical types for which this type of theory would be ineffective, such as modal polyphony, contemporary, pop, and any non-western/non-European musics based in any musical system other than common-practice tonality. Those who have read any of Schenker’s work know that he was not one to mince words, and he immediately dismissed works that did not fit within his theoretical system. What remained in the canon of “real music” was essentially written entirely by the German Classicists and Chopin.
There is also the inevitable danger that this sort of musical positivism will result in prescriptions for how music should be written. Speaking purely from my own experiences and anecdotes from colleagues, it is not at all rare to be subjected to admonitions from teachers and peers regarding the ways in which music you have composed does not do what “real music” does. “Real music has a goal.” “Real music uses the least musical ideas to say the most.” “Real music has structural unity.” Without getting into the metaphysics of reality, even if there were such a thing as “real” music (as opposed to “ineffective” music), it does or has nothing. The danger is that an entire generation of composers ceases to innovate and express themselves in favor of mimicking subjective a priori constructs, all in the name of adherence to principles that are seemingly inherent in good music. In reality, these qualities are subjective interpretations rather than objective truths. Though the sort of fire-and-brimstone rhetoric used here might seem extreme, it is a very real concern. It is the difference between saying “My music sounds like Ligeti’s because I like his music,” and “My music sounds like Ligeti’s because both adhere to principles of good musical composition.” The first is a subjective comparison, but the second supposes some underlying musical “truth.” In short, composers should not feel pressured to write in a way such that aesthetic and creativity are subservient to the canon of “real music.” The result of this pressure is dozens upon dozens of indistinguishable, vaguely avant-garde musical works that check all the boxes for what good contemporary music does.4 We should, of course, study music that we perceive to be successful or satisfying and synthesize some of its musical elements into our own lexicon. However, we should avoid actively creating a contemporary canon of “real” music; each individual work is its own unique experience, and whether or not it is “good” is entirely subjective. By remembering that qualitative and structural assessments are inherently constructs of the listener, we avoid the stagnation of our own musical culture and encourage growth and experimentation among the body of practicing musicians.
Let me state the obvious: no one should be punished or criticized for liking or disliking anything. It is not my goal to force anyone to like the music I like nor to stop anyone from stating that they do not like it. I believe one of the beautiful things about music is the non-universality of appreciation, that no one work is unanimously adored by all. However, it is important to realize that if you do not like a certain work or style of music, that is not a property inherent in the music but rather a property inherent in you. We are well past the point in musical history where we should be tolerating broad generalizations of what music is and is not based upon an individual’s propensity to like or understand that music. After all, any and every property and concept that can be perceived in a piece of music must first be present in the mind of the listener. We should all have the courage to state that we do not like something, but we should also have the courage to understand that this is not because of a property of music, but rather a property of ourselves.

Footnotes
1 I certainly do not mean to suggest that generalizable musical forms do not exist within the body of extant musical works. Clearly, many of the formal archetypes we discuss in theoretical circles are prevalent and recurring throughout musical history. My argument is simply that the perception of a work “having” or “being in” one of these archetypes relies on abstract knowledge of it in the first place.

2 Wallace Berry, Form in Music: An Examination of Traditional Techniques of Musical Form and Their Applications in Historical and Contemporary Styles (Prentice-Hall, 1986), 447–49.

3 I have no doubt that many theorists reading this might be mortified by this oversimplification of Schenkerian theory, but it is not my desire here to discuss all of its nuances, nor is it necessary to do so in order to make my overarching point.

4 Key clicks are apparently high up on this list.

0 Comments

Klang in 2018 - Updates, News, Changes

1/3/2018

2 Comments

Hello, readers. I wanted to let you all know that I'm making some changes to KLANG in the coming year. I'm hoping to start posting more regular content in 2018, and I am bringing on guest writers to bring a fresh perspective to experimental contemporary music.

One major change that I have decided to make is the "Early Reflections" section dedicated to interviews with emerging composers will have much better representation of marginalized voices in the new music community. As much as I love the music of a lot of white guys, there are plenty of women and people of color in the new music world, and their art deserves to be listened to, understood, and discussed just as much as anyone else's.

Additionally, I have recently begun a series of reviews of CDs by New Focus Recordings. Moving forward I will continue these reviews, and will start to add reviews of concerts, festivals, upcoming events and any other activities and releases of new music related to the "fringe" music to which KLANG is dedicated.

So in short, for those of you who have enjoyed reading my musings, interviews and reviews, I hope that you continue to make regular visits, as well as share these articles with your friends and colleagues. With any luck, this little project I started in late 2013 will become a helpful outlet for composers, performers, researchers, and all fans of contemporary music that doesn't always get a wide amount of exposure.

Thanks for reading.

2 Comments

Pitch Multiplication

8/28/2017

6 Comments

In this post I’m going to talk about pitch multiplication - a topic related to pitch organization that for a very long time I found to be equally fascinating and perplexing. I first came across the term around 2011 or 12 when I first started studying Pierre Boulez’s music intensely, but I never took much time to really research the topic to understand it. To be fair, I was more concerned with Boulez’s use of instrument color, orchestration, gestural language and his writings on music. Though pitch structure was (arguably) a primary compositional element of Boulez’s music (and overall philosophical approach), I was never really interested in the theoretical underpinnings of how he created pitch structures. As a result, I never fully understood how pitch was organized in some of my favorite works (Eclat, Pli Selon Pli, Third Piano Sonata).

This isn’t to say I wasn’t interested in integral serialism or systematic ordering of pitches, it’s actually quite the opposite. I was just more interested in approaches by Xenakis, Berio, Robert Morris, and (my own teacher) Mikel Kuehn. Around 2014, my focus and interests in Boulez’s music started to shift and I refocused my attention on understanding his methods of inventing and working within rigorous mathematical pitch structures, but this was still mostly related to his method of integral serialism.

However, it wasn’t until late 2016 that I really began looking into pitch multiplication, as previous attempts were always unfruitful. I guess my background in math just wasn’t what it needed to be, or maybe I was just having issues wrapping my brain about the concept, because what I ultimately discovered is that the math is quite simple, I was just making it harder than it needed to be.

All of that aside, this leads to the main question at hand - what is pitch multiplication? Not only that, but how can it be used in a meaningful way that doesn’t render it an academic or theoretical exercise? The simplest explanation is that pitch multiplication is the act of multiplying one pitch class set with another, with the resultant product being a superset of pitch classes. This can be broken into simple multiplication and complex multiplication. In this post I will only be looking at simple multiplication and provide some examples, but I will also provide links for further reading related to complex pitch multiplication. I will also discuss some of the history of pitch multiplication and where it came from before diving straight into the mathematics behind the process.

Sidebar: the following information is taken primarily from Stephen Heinemann’s articles on pitch multipliation and Lev Kablyakov’s writings on multiplication in Boulez’s Le Marteau sans Maitre.

First a little bit of terminology:

Multiplicand - element x in the equation x * y = z
Multiplier - element y in the equation x * y = z
Product - element z in the equation x * y = z; the result of multiplying two elements together
Normal form - ordered pitch class set in which the total interval content is the most compressed
Initially ordered pc set (IP) - a pc set in which the first pitch is ordered, but the pcs that follow are not
Initial pitch class (r) - the first pc in an initially ordered pc set (important for determining OIS)
Ordered pitch-class interval structure (OIS) - interval set of an ordered pc set, determined by finding interval of initial class to other pcs in the set: given set (5,9,0), OIS = (<5,5>,<5,9>,<5,0>) = (047)

Pitch multiplication is a technique that was invented by Pierre Boulez as a means of creating variations of ordered and unordered pitch class content beyond the rules and guidelines of integral serialism. By the mid 1950s, many serial composers began moving into new territory and added individualized procedures to their approaches to serialism (aleatory, electronics, graphic notation, new approaches to ordering procedures). Pitch multiplication was one of Boulez’s primary compositional techniques that individualized his style that was characteristic of pieces from the 1950s and 60s, particularly his masterwork Le Marteau Sans Maitre. For Boulez, the practice of pitch multiplication allowed the composer to create ordered pitch class sets according to some kind of logic or rules, multiply the two together, resulting in a numerous supersets that could undergo other ordering procedures; the main point being that Boulez was able to create interrelated supersets from a small amount of pitch class set material, all of which could be ordered further by whatever scheme he chose. This approach could allow a composer to generate a massive amount of pitch material from a relatively limited starting point. It could potentially allow for repetition of pitches, depending of how the composer chose to filter the results of the superset (Boulez would remove repeated pitches, but one could leave repeated pitches in the final superset).

The earliest recorded example of pitch multiplication resulting in a superset from multiplying two pitch class subsets is Nicholas Slonimsky’s book Thesaurus of Scales and Melodic Patterns, which contained 1300 scales and patterns constructed with a type of pitch multiplication. Slonimsky created his patterns by taking a pitch class set, for example set X = (0134), and multiplying it by another, let’s say set Y = (015). The end result would look like this:

(0134) (015) = <0,1,3,4,1,2,4,5,5,6,8,9>

Notice resulting superset is an ordered set that allows for repeated pitches. The superset is created by transposing set X by each element of set Y. This would be shown as the following:

A = T0 (0134) = {0,1,3,4}
B = T1 (0134) = {1,2,4,5}
C = T5 (0134) = {5,6,8,9}

The results of the transposition are then joined as A B C to create the ordered superset:

{0,1,3,4,1,2,4,5,5,6,8,9} as shown above

The notated result would look like this

Example 1

It’s important to notice that Slonimsky allows for repeated pitches and creates his scales/patterns by ordering set X by transpositions of set Y. While the end result can be found through a process of pitch multiplication, it is not the same application as applied by Boulez, thought it is successful at creating a sequence of pitches related by interval interval with transpositional variation within the sequence. It is an elegant method for creating scalar pitch collections.

Other examples of pitch multiplication can be found in Stravinsky and Lutoslawski (as examined by Heinemann in his articles, linked below), although these examples outline the theoretical concept of multiplicative relationships among pitch class sets, and were not intentional practiced by the composers. Boulez was the first composer to intentionally theorize, invent and apply his approach to pitch multiplication. We won’t look at the examples in Stravinsky and Lutoslawski, but if this topic is interesting to you beyond Boulez or other simple applications I strongly suggest looking into Heinemann’s article.

Lets take a closer look at calculating supersets with pitch multiplication. The method employed by Slonimsky works as a method, but again it generates ordered transpositions of a single set. Another method more closely related to Boulez’s method is to create a Cartesian product of the two pc sets. A Cartesian Product is the product of two sets made up of each pair of the elements. For ease of reference we’ll call (0134) set X and (015) set Y. A Cartesian product of set X containing elements (a,b,c,d) and set Y containing elements (x,y,z) is {(a,x),(a,y),(a,z),(b,x),(b,y),(b,z),(c,x),(c,y),(c,z)}. The example below puts this into context with numbers

Example 2

The equation for creating a Cartesian Product: Set X Set Y = {(x+y) mod 12 | x X y Y}

Set X = (3479)
Set Y = (035)
Set X * Set Y =
{(3,0),(3,3),(3,5),(4,0),(4,3),(4,5),(7,0),(7,3),(7,5),(9,0),(9,3),(9,5)}

Each pair is then summed at mod12, resulting in the following set:
        (3,0) = 3
        (3,3) = 6
        (3,5) = 8 ...
      Total = {3,6,8,4,7,9,7,A,0,9,0,2}

This can now be used as an ordered set, as Slonimsky would, which would look like this:

or we can remove duplicate pitches, and put the set in normal order:  = {6,7,9,A,0,2,3,4}

The result of this multiplication process provides an 8-note collection that can be used in numerous ways; 8 notes of a scale, the superset broken into subsets, undergo a process of transposition to extend it’s use, etc. Additionally, it could be used as an intermediary superset between two moments in a piece. The product of the multiplication contains pitch classes 2, 6 and A, none of which are contained in either set X or Y, thus the augmented chord <2,6,A> could be used as an arrival point from the a process of moving through sets X and Y.

The Cartesian Product method of multiplying pc sets is simple and straight-forward, but the application of the process as described by Boulez takes on another level of specificity, specifically ordering the sets. This is process that Heinemann describes in his dissertation on pitch multiplication in the music of Boulez. This method involves taking two sets, again X and Y, using set X as the multiplicand and set Y as the multiplier, and determining the product of the two based on an ordered interval series of set X. Let’s break all of that down, by first finding the ordered pitch-class interval structure (or OIS as defined by Heinemann) of a set:

Example 3
Set X = {2,3,6,7}, put in ascending order for simplification of the explanation
Set Y = {2,5}

For this example we’ll assume that {2,3,6,7} is the order of the set. We’ll look at different orderings in examples below

Step 1 - find the ordered pitch-class interval structure, and finding the interval relationship of each element to the first element in the set:

Set X = {a,b,c,d}, OIS = (i<a,a>,<a,b>,<a,c>,<a,d>)
Set X = {2,3,6,7}, OIS = (i<2,2>,<2,3>,<2,6>,<2,7>) = (0,1,4,5)
NOTE: the first interval class will always be 0 in an OIS

Step 2 - Use elements of set Y as transposition levels for the OIS of set X

Set X Set Y = {2,3,6,7} {2,5}
{2,3,6,7} = {0,1,4,5}
T2 {0,1,4,5} = {2,3,6,7}
T5 {0,1,4,5} = {5,6,9,A}

Step 3 - Join the results together, remove any duplicate pitch classes, put in ascending order

{2,3,6,7} + {5,6,B,0} = {B,0,2,3,5,6,7}
The result of step 3 is the product of {2,3,6,7} * {2,5}

Let’s take this a step further. Because this method of pitch class multiplication involves ordering set X, we are able to get different results depending on the order of the multiplicand. For this we’ll need to take the ordered. It is important to remember that sets X and Y MUST BE IN NORMAL FORM, but beyond that they can be re-ordered for the process of multiplication. For this extension of the technique, concept of initially ordered pc set and initial pitch class (r) become important. Given sets X and Y, either can be the multiplicand and multiplier, but let’s stick with X as the multiplicand for now.

Example 4
Set X = {6,0,9,7}, in normal order is {6,7,9,0}
Set Y = {2,5}

We can use the normal order of the set for the multiplicand or rotate the set
In normal order, the value of r is 6, and the set is written as {6<7,9,0>}. When rotating and changing the value of r, the order of the pitch classes are also reordered. The following are the four permutations of Set X through rotating each pc to the value of r

Ordered sets:       6,<7,9,0>}   {7,<9,0,6>}   {9,<0,6,7>   {0,<6,7,9>}
OIS:       {0,1,3,6} {0,2,5,B} {0,3,A,B} {0,6,7,9}

Having these sets now allows us to create new products using set X as the multiplicand. If set Y remains the multiplier, we can use the OIS from each permutation of set X as the multiplicand and get the following:


Example 5
{6<7,9,0>} {2,5}
{6,<7,9,0>} = {0,1,3,6}
T2 {0,1,3,6} = {2,3,5,8}
T5 {0,1,3,6} = {5,6,8,B}
{B,2,3,5,6,8}

{7<9,0,6>} {2,5}
{7,<9,0,6>} = {0,2,5,B}
T2 {0,2,5,B} = {2,4,7,1}
T5 {0,2,5,B} = {5,7,A,4}
{A,1,2,4,5,7}

{9<0,6,7>} {2,5}
{9,<0,6,7>} = {0,3,A,B}
T2 {0,3,A,B} = {2,5,0,1}
T5 {0,3,A,B} = {5,8,3,4}
{0,1,2,3,4,5,8}

{0<6,7,9>} {2,5}
{0,<6,7,9>} = {0,6,7,9}
T2 {0,6,7,9} = {2,8,9,B}
T5 {0,6,7,9} = {5,B,0,2}
{8,9,B,0,2,5}

Additionally, we can also use set Y as the multiplicand and set X as the multiplier. However, in this instance set X must remain in normal form, and set Y must be converted into an OIS. The example below demonstrates this process

Example 6
Ordered Y Sets: {2,<5>}   {5,<2>}
OIS: {0,3}       {0,9}

{2,<5>} {6,7,9,0}
{2,<5>} = {0,3}
T6 {0,3} = {6,9}
T7 {0,3} = {7,A}
T9 {0,3} = {9,0}
T0 {0,3} = {0,3}
{6,7,9,0,3}

{5,<2>} {6,7,9,0}
{5,<2>} = {0,9}
T6 {0,9} = {6,3}
T7 {0,9} = {7,4}
T9 {0,9} = {9,6}
T0 {0,9} = {0,9}
{3,4,6,7,9,0}

At the end of the process we have a total of 6 new supersets from the result of multiplying two sets from one another. These can now be used as ordered sets for melodic writing, they can be used as unordered sets to determine harmonic structures. They could be used as unordered sets and be applied free to both melody and harmony to have a consistent pitch structure throughout a section. They could be used as blocked chords and with some working out one could find smooth voice leading to get from one chord to the next. If we were Boulez, we would probably establish some kind of localized ordering scheme and use each of these as unordered sets to be filtered through whatever ordering systems is applied to the overall piece, section of the piece, etc. The example below shows these chords in standard notation to show the sets in a musical context.

(Chord spelling used for visual assistance, to keep noteheads from stacking on top of one another; no ordering melodic or vertical ordering is implied by the voicing)

   While the above method uses simple math, it can be a little cumbersome and not always clear to see. Heinemann demonstrates another method for deriving supersets, that might be a preferred method for someone more used to looking at pitch matrices. The example below demonstrates how th matrix method works using the same pc sets and OISs:

Example 7
Ordered sets:    {6,<7,9,0>}   {7,<9,0,6>}   {9,<0,6,7>   {0,<6,7,9>}
OIS: {0,1,3,6} {0,2,5,B} {0,3,A,B} {0,6,7,9}


   0    1    3    6
2| 2    3    5    8
5| 5    6    8    B
                      Total = {B,2,3,5,6,8}


                          0    2    5    B
                      2| 2    4    7    1
                      5| 5    7    A    4
                  Total: {A,1,2,4,5,7}

                          0    3    A    B
                      2| 2    5    0     1
                  5| 5    8    3     4
                      Total: {0,1,2,3,4,5,8}

                  0    6    7    9
                        2| 2    8    9    B
                        5| 5    B    0    2
                        Total: {8,9,B,0,2,5}

As you can see, both methods yield the same results. It pretty much comes down to the method you prefer: equations or matrices, either way you’re doing basic addition and mod12.

The example below shows these used in a musical framework to demonstrate how I might go about using the results of the multiplication.

So that’s simple pitch multiplication. Hopefully this blog entry cleared up any confusion you had before, and if you’ve made it this far and still want to know moe I suggest you check out the Heinemann and Kablyakov articles below. There is plenty more to uncover with this technique and Heinemann and Kablyakov do it more justice than I can here. That said, I strongly encourage you to try this method. It doesn’t have to just be used for atonal collections, you could choose to utilize more consonant pitch collections, which can then be manipulated in various ways to sound more consonant when used melodically or harmonically. One could also utilize these for their ordered properties and filter out anything that doesn’t fit within a given superset. The possibilities are endless, and for that reason one could see why Boulez was so drawn to this technique.

6 Comments

35 Composers All Undergrads Should Know

3/22/2017

2 Comments

I think it’s fair to say that 20th and 21st century music don’t always get a fair amount of coverage in terms of music history and theory courses, specifically at the undergraduate level. I understand this is partially because of the wide variety of styles and developments that took place during the 20th century, but I still feel it is problematic that so much is left out. The musical developments of the 20th century, specifically the latter half of the 20th century, shaped our modern approaches and conception of music and art in popular genres and concert music, yet so little time is devoted to the study of that music.

I don’t feel that 20th/21st century music should dominate music history/theory curriculums, and I can only speak from personal experience, but I feel that a large majority of American music students are lacking in their knowledge of 20th century music beyond Stravisnky, the 2nd Viennese School and American minimalism. As an undergrad I learned about Debussy, Shoenberg, Webern, Berg, Bartok, Stravinksy, Shostakovich, Prokofiev, Ives, Poulenc and Copland in detail. After that unit of early 20th century music we jumped through Messiaen, mentioned that Darmstadt was a place that existed, learned a lot about American minimalism (at least Glass and Reich) and then finished a superficial passing of composers from ~1975-present.

That said, I don’t really have a solution for this problem, and I understand developing new courses and changing curricula is a long and difficult process. However, there are so many composers that I personally think all undergraduate students should know about, especially if they plan to continue with graduate studies in music. I have narrowed this list down to 35 composers who, if I had my druthers, would required information for all undergraduate history and theory courses. Below is my list of composers as well as a short rationale for each:

…but before we get started

Honorable Mention
These are composers I feel could be on this list, but excluded them because they seem to receive more coverage in undergraduate courses, and are performed more frequently. This, however, is based solely on my own undergraduate experience and my observation of other undergraduate curriculums I experienced through my graduate and doctoral studies.

Elliott Carter
Olivier Messiaen
John Cage
Philip Glass
Steve Reich
John Corigliano
John Adams

And, in a perfect world, I would prefer to teach two courses - early 20th century and late 20th/21st century history - which would include the following composers:

Ruth Crawford Seeger
Carl Ruggles
Witold Lutoslawski
György Kurtág
Toru Takemitsu
Alfred Schnittke
Ben Johnston
Stuart Saunders Smith
John Luther Adams
Joan La Barbara
Brian Ferneyhough
Tristan Murail
Claude Vivier
Libby Larsen
Salvatore Sciarrino
Laurie Anderson
Chaya Czernowin
Jennifer Higdon
David Lang
Julia Wolfe
Michael Gordon
Unsuk Chin
John Zorn
Kevin Puts

.......but we don't live in a perfect world, so let's move on
___________________________________________

The 35 Composers

Edgard Varese - emancipator of noise and sound; key figure in the early 20th century avant-garde, made major impact on electronic music (58 Brussels’ World Fair) , truly unique figure who influenced so many facets of music of the early, mid and late 20th century

Pierre Boulez - arguably one of the most frequently performed and awarded musicians on the 20th century, very skilled conductor, virtuoso pianist, innovative composer, knowledgeable theorist and musicologist; we should get past the mistakes of his youth and give his work the respect it deserves

Luciano Berio - Composer who balanced the lyricism and with the sound world and integral serial methods of the Darmstadt school (in early works), later works showing more eclecticism of style marked by post-Modernist composers, but with the gestural and harmonic language that grew out of Darmstadt. Berio also did some pioneering work in electronic music and text-sound composition; at a minimum one should know the Sequenzas

Karlheinz Stockhausen - Like Boulez, Stockhausen was one of the most influential musical figures of the 20th century, but Stockhausen’s influence (especially in electronic music) reaches into popular music and experimental rock and jazz; also a talented conductor, pianist and theorist in addition to being an innovative composer

Luigi Nono - Darmstadt composer with a different approach from the total serialism of Boulez, Berio, Stockhausen, et al; Nono brings a level of narrative and expression to what is otherwise very aggressive music; highly influential on developments in Italian music of the middle and late 20th century

Milton Babbitt - Though notorious for his “Composer as Specialist,” Babbitt was an incredible teacher and composer who influenced many composers of the 20th century (including musical composer Steven Sondheim); highly influential in terms of music theory and analysis of atonal music with pitch sets, serial procedures, combinatoriality, etc.; Pioneering work in electronic music at CPEMC

Harry Partch - His life is an incredible story; arguably the most important figure in microtonal music of the 20th century, instrument maker, highly influential on microtonal music (experimental and popular)

Iannis Xenakis - Major figure in electronic music and mathematical approaches to composition with serialization; developed his own theories and approaches outlined in Formalized Music

Krzysztof Penderecki - All undergrads will know Threnody for the Victims of Hiroshima, but it’s likely that few will know De Natura Sonoris Nos. 1 and 2, Polymorphia, Anaklasis, Kanon for Orchestra and Tape, Fluorescences, and the St. Luke Passion. Not only are these beatiful works that explore color and timbre as a primary formal framing device, they are all landmark works in sound mass composition. They are also all used in various films, including The Shining, The Exorcist, Wild at Heart, Children of Men and Shutter Island. Don’t like noisy sound masses? That’s ok, because Penderecki later turned his back on experimental noise music and began writing more traditional neo-Romantic music, which is equally beautiful, albeit a little on the “old” side for my personal taste (but no one asked for that here).

Gyorgi Ligeti - Early pieces utilizing quotation and influence of Bartok and Kodaly, 50s and 60s compositions with micropolyphony, sound-mass composition, textural music based on electronic experimentation; later works showing a multitude of styles. Ligeti basically did it all, and did it well.

Morton Feldman - major figure in experimental music, developed new systems of graphic notation, influential on music and art of the 60s, 70s and 80s. Feldman is primarily important for his contributions to aleatoric and indeterminate music (also developed by his contemporaries Cage, Earle Browne and Christian Wolff). I think Cage is covered fairly well, and while I would like to see Brown and Wolff covered extensively, I would be fine with undergrads having a more than passing acquaintance with Feldman.

George Crumb - Crumb is taught to an extent, but students should know beyond Ancient Voices and Black Angels; incredibly important figure in American new music; style is without comparison in terms of sound and notation; no one writes like Crumb, but Crumb, new approaches to timbre

Peter Maxwell Davies - Later works are mostly tonal works for students, but he was an important composer in Europe, and his early stage works Eight Songs for a Mad King and Miss Donathorn’s Maggot were very influential on crossover works of music, theater and performance art

Jacob Druckman - similar to Joseph Schwantner in terms of orchestrational color and imaginative use of ensemble timbre, but Druckman encompasses a very wide range of style and aesthetic. He was highly influential on a generation of students (including Cindy McTee, David Lang, Laurie Spiegel, Aaron Kernis, Daniel Kellogg and Chris Theofonidis), and he is a great example of a composer who was heavily influenced by electronic music and the potential of new sounds available, more so than many of his post-Modernist contemporaries of the mid-late 20th century.

Mario Davidovsky - Influential composer at the Columbia-Princeton Electronic Music Center, series of Synchronisms for solo instruments and tape. Davidovsky is one of 3 composers to win a Pulitzer Prize with a piece utilizing electronics as a primary component of the piece (Synchronism 6 for piano and tape), the other two being Leon Kirchner and Charles Wuorinen.

Pierre Schaeffer - One of the earliest practitioners of elecronic music; established musique concrete, created Groupe Recherches Musicales (GRM) which is still a highly influential organization for the research and development of electronic music

Helmut Lachenmann - developed the concept of acoustic concrete, which drove entirely new approaches to acoustic composition

Sofia Gubaidulina - Incredibly skilled Russian composer who ISN’T Shostakovich (nothing against, him, but Russian music did continue after Dmitri…); lots of use of quotation, mixing of styles, use of improvisation techniques, exploration of interesting timbres. Gubaidulina has also received numerous awards for her music, and is somehow still not a household name among 20th century composers.

Julius Eastman - I know we’ve all heard of Glass, Reich, Riley and Young, but Julius Eastman is rarely, if ever, talked about in classroom discussions of minimalism, which is really terrible. Eastman was an amazing performer (singer and pianist) and a brilliant composer whose life and work were cut entirely too short. If you’re looking for some minimalism with a little grit and a lot of depth, maybe put down Reich/Glass and pick up some eastman.

Pauline Oliveros - Founding member of the San Francisco Tape Music Center and the founder of Deep Listening. Oliveros is a highly influential composer and innovator of electronic music who taught at numerous institutions including Mill College, San Diego State University, Oberlin, and the Rensselaer Institute.

Terry Riley - I know I just said we all know about Teri Riley, but really most people just know about In C, which is undeniably influential, and is a lot of fun to perform. That said, Riley’s music is heavily influenced by jazz and Indian classical music, and much of his work outside of In C shows that cross-cultural influence, which became important to the ritualistic aspect of cell-based minimalism. Riley also did important work at the San Francisco Tape Music Center.

La Monte Young - Another composer associated with classical minimalism who existed well outside of that aesthetic, Young was very active in experimental music and performance art, specifically his work with Fluxus. Young’s work was also very influential on John Cale and his work with the Velvet Underground, and helped to pioneer the practice of ambient drone music.

Meredith Monk - Lots of important work in performance art, has received numerous honors and awards for her contributions to contemporary art, music and theater, often works on interdisciplinary multimedia works that stretch genres and has received recognition in the popular music and film world.

Frederic Rzewski - American composer who is often associated with minimalism based on the surface repetition, but Rzewski’s music contains a level of subtlety and improvisation that is not often found in the classic minimalism of Glass and Reich, but is more similar to that of Riley and Julius Eastman (contemporaries of Rzewski). Rzewski’s music is also marked by its association with topics of social and political activism.

Charles Wuorinen - I don’t think Charles Wuorinen ever was, or will be, a household name, but he’s definitely a composer that all undergraduates - especially composers - should have at least a passing knowledge of. While most of Wuorinen’s output could be defined as coming from the 12-tone and serialist tradition, and although he can sometimes be a curmudgeonly old man, his music is vastly rich and deep, and I feel that it has stood the test of time. Additionally, he won a Pulitzer Prize for his piece Time’s Encomium in 1970, the only Pulitzer Prize awarded to an entirely electronic work. It should also be noted that Wuorinen wrote what was at one time a very influential composition book, and he had numerous students that would later become highly successful composers (Arthur Russeell, Michael Daugherty, Aaron Jay Kernis)

Robert Morris - Possibly better known in the theory world, but Robert Morris is an incredibly brilliant musician and a very creative composer. His works are not limited to mental gymnastics of serial and post-serial technique, but are full of expressive beauty and nuance. His outdoor pieces are also incredibly creative works that utilize large outdoor spaces and spatialized ensembles to create immersive sonic events. He was also on faculty at Eastman (along with Schwantner and Sam Adler) and had his own flock of dedicated and talented pupils.

Kaija Saariaho - Arguably one of the most frequently performed composers of the late 20th and early 21st centuries. Saariaho’s music sits somewhere between post modernism and spectralism, but regardless of what genre you want to put on it, the music is crafted masterfully, satisfies modernist interests in complex “systematic” atonality (not serial in any way, but not freely atonal) and is simultaneously hauntingly expressive. Saariaho also has many works that are major pieces for instruments and electronics including Pres for cello and electronics, Noanoa for flute and electronics and Nymphea for string quartet and electronics.

Arvo Pärt - The Estonian king of holy minimalism. Arvo Part’s music is rich and beautiful, but it is also important for being influential in what is now referred to as holy minimalism (along with Henryk Gorecki and John Tavener), a style which utilizes the repetition associated with American minimalism, but with the pacing and mood of choral music, or at least more chorale-like textures. Part is often considered the originator of this approach to minimalism, and his instrumental and choral works in this style are performed frequently throughout the world.

Gerard Grisey - French composer credited with developing spectral composition along with his colleague Tristan Murail. Spectral music was a major development in composition that led to influences in orchestral and chamber music as well as electronic composition (with and without instruments) and film music. In my personal opinion Grisey should be included with Debussy, Les Six, Messiaen and Boulez in terms of his importance to French music and contemporary composition on the whole.

Louis Andriessen - Andriessen’s mature musical style is oten associated with minimalism because of its use of repetition, but it is highly influenced by jazz and simultaneously by the spectral techniques of Claude Vivier. While many minimalists chose to utilize pitch structures related to tonal and modal harmony, Andriessen’s music favors crunchy European dissonance and pitch structures based on the natural overtones series. Andriessen also utilizes odd combinations of instruments instead of more traditional chamber groups or orchestras

Joan Tower - A major figure in the development of late 20th century American music. Tower was also a performer and was a founding member/pianist of the Da Capo Chamber Players. Her music has received numerous awards including a Grawemeyer for Silver Ladders. Other important works include Sequoia, Petroushskates and Fanfare for the Uncommon Woman

Frank Zappa - Frank Zappa is, in my opinion, one of the most interesting and talented musical minds of the 20th century. He never formally studied music or composition and could write chamber and orchestral works on the level of Varese, Stravinsky, Berg, Boulez, you name it. He also wrote interesting genre bending popular music in numerous styles, experimented with electronics (having composed numerous fixed media electronic compositions), he worked at IRCAM, was one of the first people to own a personal Synclavier, and arguably influenced music in popular music and contemporary concert music to a greater extent than anyone on this list.

Ellen Taaffe Zwillich - The first woman to win a Pulitzer Prize (1983 for Three Movements for Orchestra, Symphony No. 1), first person to hold the Composer’s Chair at Carnegie hall, a massive list of honors and awards, four Grammy nominations, chair of the BMI Student Composer Award (following Milton Babbitt and William Schuman). Zwillich’s music and career should be taught in all 20th century music history courses, without a doubt.

Shulamit Ran - The second woman to win a Pulitzper Prize (1990 for Symphony), recorded by over 12 record labels, numerous honors/awards and five honorary doctorate degrees. Shulamit Ran teaches at the University of Chicago and has been a leading voice in contemporary music throughout the world and her approach to composition is influenced by her studies with Norman Dello Joio, Ralph Shapey and Elliott Carter. This led to a compositional voice characterized by eclecticism of style, harmonic and rhythmic language.

Augusta Reed Thomas - A talented composer who could be described as balancing postmodernism and neo-Romanticism. Thomas was very talented as a young composer and became a tenured professor at Eastman at the age of 33, but later went on to teach at Northwestern. Thomas has composed for numerous ensembles and genres, has received numerous awards and commissions and is frequently performed throughout the world. It is difficult to deny that she is one of the most celebrated composers of the 21st century.

Thomas Adès - I feel that Thomas Adès’ music is similar to Augusta Reed Thomas in terms of style and aesthetic, and I personally feel that I could not include Augusta Reed Thomas without Thomas Adès or Adès without Thomas. His music also demonstrates his approach to post-modernism with eclecticism of style, pastiche, quotation and colorful instrumentation.

2 Comments

Another Reflection on 2016

1/5/2017

0 Comments

As we all know, 2016 was not an easy year for a multitude of reasons. I always spend the last couple weeks of December reflecting on the year (as I imagine a lot of people do), and I thought back to my first KLANG post of 2016 (posted on this day one year ago). I couldn’t remember what it was, so I opened up my computer and checked the website. Sadly, it was my “Remembering Boulez” post, which was not a stellar way to start the year, but it was a post that needed to happen in the immediate aftermath of learning of Boulez’s passing.

The problem was that it did not stop there. Over and over again 2016 took from the world one musician after another. Concert music, electronic music, experimental music, popular music, jazz, folk music, nobody seemed off-limits in 2016, and it was definitely a year that took a lot of important musicians and composers who helped shape the musical landscape of 2016. Here is (very) short list of some of the composers lost in 2016:

Pierre Boulez (Jan 5, 90)
Leslie Bassett (Feb 4, 93)
Steven Stucky (Feb 14, 66)
George Martin (March 8, 90)
Peter Maxwell Davis (March 14, 81)
Tony Conrad (April 9, 76)
Jean-Claude Risset (Nov 22, 78)
Pauline Oliveros (Nov 25, 84)
Karel Husa (Dec 14, 95)

On a more personal note, I felt directly impacted by the passing of so many of the composers on this list. While I did not know any of these composers personally on a personal level (I had met and spoken with Steven Stucky on multiple occasions, but always under professional circumstances), their music, writings and lectures were a huge influence on me as a young composer searching for my own artistic voice.

Karel Husa was a composer who sparked in me a new interest in the wind ensemble within the last couple of years, and while I’ve never been incredibly interested in the ensemble or literature I always found his music wonderfully imaginative in substance and orchestration. Pauline Oliveros and Jean-Claude Risset, who died only a few days apart, were massive influences on me in my early studies of electronic music at Ohio University. Rissets Songes for instruments and electronics is still one of my favorite early works for instruments and electronic sound and Oliveros experiments with electronics are still of particular interest for me. Additionally, Oliveros’ philosophy and method of deep listening had a huge impact on how I listen to the world around me.

Tony Conrad ignited in me a new interst in minimalism around 2008/09. While there was a time in my early studies when I appreciated Glass, Reich and, to the greatest extent, Terry Riley, I was never really taken by minimalism. That is until I heard Conrad's album Slapping Pythagoras with all of its beatiful and noisy repetition of cells and drones. This album would later get me interested in more gritty and abrasive (at least in comparison to "classic" minimalism) forms of minimalist music that I didn’t find in the works of Glass, Reich, Riley or even La Mont Yonge (nothing against those guys, though). These included Julius Eastman, Louis Andriessen, Julia Wolfe and Frederic Rzewski.

Peter Maxwell Davies was one of the most influential composers on my musical thinking as an undergraduate at Ohio University. I first found his Eight Songs for a Mad King when I was a sophomore and I listened to the Unicorn recording with Julius Eastman while following along with the score more times than I could possibly even remember. I even attempted to model my undergraduate thesis after Davies’ work by writing a monodrama for baritone voice and Pierrot ensemble. Though I fell far short of the mark with my own composition, I will never forget the massive influence that Davie’s piece had on me, as well as Miss Donnithorne’s Maggot, in forging my interests in the intersections of music and theater.

George Martin almost goes without saying. I was never a huge fan of The Beatles (I know, blasphemy, right?), but I did like the later more experimental records. It was years later that I found out about the influence of George Martin and the recording and studio techniques he employed that made those records so special. Not to take anything away from The Beatles, but for me it was the studio experimentation that makes some of those songs so special and interesting. Additionally, Martin brought the idea of the studio as an instrument (an idea that had been in practice in Europe and American universities for years) to the world of popular music. His genius as a recording engineer was not limited to polished recordings, and he is someone I’ve always looked up to in term of creative recording technologies.

Steven Stucky and Leslie Bassett are two composers who I don’t really align with aesthetically, but as an undergraduate I loved studying their music, specifically for the orchestral color. I was all about drawing aesthetic lines in those days of my studies - “I’ll listen to this because it’s atonal, but that’s not thorny enough, yada yada yada….”. But Bassett and Stucky were different. I would listen to Stucky’s Ad Parnassum over and over again. Bassett’s Variations for Orchestra was one of my favorite pieces at a time when all I wanted to listen to was Babbitt and Stockhausen. It was also through Bassett that I became familiar with the work of Robert Morris, who would later be very influential on me during my graduate studies.

When I was working toward my master’s at Bowling Green State University I had the opportunity of meeting Steven Stucky. Though I saw him around the building numerous time, I only had one opportunity to spend any quality time speaking with him - the 2010 BGSU New Music Festival. During that festival we met and talked 3-4 times over the course of 3 days. My favorite moment was at an after-party following the last concert of the festival in which everyone gathered at a small bar in downtown Bowling Green called DiBenedetto’s for drinks and festival talk. I went up to the bar to get a refill on my whiskey and I saw Stucky standing, also waiting patiently for a refill. I walked up to him and congratulated him on the performance of his new piece Isabelle Dances and told him it was nice having met him (we had already talked 2-3 times at this point during the festival). He reached over and patted me on the back and said “It was nice meeting you too, Jon. You’re a good kid. Hopefully we’ll see each other again the next time I’m here.” Then we clinked our glasses together, took a drink and parted ways into the crowd.

That brings us to Pierre Boulez, definitely the hardest hit for me on this list. I won’t spend much time talking about that here, since I dedicated an entire post to reflecting on Boulez a year ago on the day of his passing. I can say that Boulez’s music is still a primary influence on my own work, his writings (yes, even the early polemical ones) have been important in the shaping of my own musical thinking, and I feel that he has written some of the richest and most emotionally moving music I’ve ever had the pleasure of experiencing. He will also be dearly missed, and I cannot emphasize enough the impact that he had on 20th century music. Whether you love him or hate him, you cannot deny his importance on new developments in musical thinking, composition, discourse and performance.

And with that I think I’ll stop. I apologize for starting both 2016 and 2017 with downer posts, but I felt it necessary to do a reflection on the impact of those that were lost in 2016, both for the music world at-large and for me personally. Let’s hope that 2017 is a little more forgiving. Below is a list of performers and composers in the popular music world I also felt were major losses, at least for me personally. You will all be missed, and thank you for your contributions to the developments of music in the 20th and 21st centuries.

Leonard Cohen
David Bowie
Prince
Merle Haggard
Maurice White
Glenn Frey
Paul Kantner
Greg Lake
Keith Emmerson
George Michael
Pete Burns
James Woolley
John Berry
Phife Dawg

0 Comments

Creating Pitch Structures with Sieves

9/13/2016

4 Comments

Heads Up: the following entry contains a lot of set theory. For the sake of avoiding confusion, when referring to pc sets I will use A to represent the integer 10 (A#/Bb) and B to represent the integer 11(B-natural)

I’ve always felt that one very useful benefit of the tonal system, even when highly chromatic, is that it contains built-in restrictions one must follow in order to adhere to the system successfully. Even a highly chromatic tonal work must, by definition, center around some kind of tonic, and any progression toward or away from that tonic is governed by a series of loose guidelines governed by the hierarchical relationship of scale degrees and chords to the tonic. The same cannot always be said of atonal music, especially atonal music based around pitch-class sets (pc sets). The composer must create his or her own restrictions in order to establish a unifying harmonic/pitch language within a work. This is not impossible, and there are countless organizational methods that composers have used throughout the 20th and 21st centuries; use of symmetrical sets, limited transpositions of a single set, serial procedures, Messiaen’s modes of limited transposition, and others. One method that (I believe) is lesser-known is the use of sieves, developed by Iannis Xenakis, Greek composer, architect and music-theorist. Xenakis was a pioneer in the use of applying principles of architecture and stochastic processes to his music through mathematically calculated pitch and rhythmic systems. Sieves can applied to rhythmic structures and pitch structures equally, but I will only be going over how to apply a sieve to pitch (a post on rhythm is in the works). I will discuss what a sieve is, how it is constructed, how it can be mapped to pitch and some of the benefits that can be gained from using this particular method of pitch organization.

In simple terms, a sieve is a means of filtering. Mathematically speaking, it is the filtering of a set of numbers based on specific rules so that only some members of the set remain. Christopher Ariza defines a sieve as a formula consisting of one or more residual classes combined by logic operators. A residual class consists of two integer values, a modulus (M) and a shift (I). The modulus can be any positive integer greater than 0, and the shift can be any integer from 0 to M-1. A modulus and shift will be notated M@I (read modulus “M at shift I).

Another way of notating a sieve is to represent it as as an integer (the factor or modulus) with a subscript integer to represent the shift. An example is 30, which represents the series [0, 3, 6, 9, 12…]. We can alter the shift and make it 31 to create the series [1, 4, 7, 10, 13...]. You can also combine two series together to create a new compound series. Take, for instance the following:

32 + 42 = s, in which s is the composite set of the two subset sieves

32  = [2, 5, 8, 11, 14…]
42  = [2, 6, 10, 14…]
      S = [2, 5, 6, 10, 11, 14…] and the set continues

The example above is what we call a symmetrical periodic set. The two elements (32 and 42) are individually periodic sets, and when combined together they form the interval series [3,1,2,1,3], which is a symmetrical set. When the two residual classes have the same shift you can find their periodicity by multiplying the two factors. In this case 3 x 4 = 12, so every 12 integers each of the sets will be replicated, and therefore their superset [2,5,6,10,11,14] will be replicated. The shift value of 2 indicates that the series will replicate at every 14th integer (a period of 12 with a shift of 2 = 14).

If we combine two residual classes with the same factor/modulus but different shift values we can create a periodic asymmetrical set. Take the collection below, for example:

120 + 122 + 124 + 125 + 127 + 129 + 1211  = [0,2,4,5,7,9,11]
And with mod12 this set would be replicated following integer 11

This sieve represents the structure of a major scale. As the set replicates itself we have the same interval structure replicating itself over and over [2,2,1,2,2,2,1,2,2,1,2,2,2,1,…]. We can do the same for other scales:

Natural Minor:     120 + 122 + 123 + 125 + 127 + 128 + 1210  = [0,2,3,5,7,8,10]
Harmonic MInor 120 + 122 + 123 + 125 + 127 + 128 + 1211  = [0,2,3,5,7,8,11]
Octatonic      120 + 121 + 123 + 124 + 126 + 127 + 129 + 1210  = [0,1,3,4,6,7,9,10]
Whole-tone      120 + 122 + 124 + 126 + 128 + 1210  = [0,2,4,6,8,10]

Sieves are not limited to just the harmonic structures of the tonal system. Any set of residual classes can be combined to form a sieve that can be mapped onto pitch space. Let’s look at the example above (32 + 42), which creates the set [2,5,6,8,10,11,14]. If we extend the sequence and then map it onto a mod12 pitch class space we get the set [2,5,6,8,A,B], with a prime form of (013569). We can map this onto pitch-class space, for instance the range of a piano, and we get the following series:

This brings me back to my opening remarks about the built-in restrictions of the tonal system being a benefit of that particular harmonic/pitch language. How do sieves help solve this problem created with atonal pitch structures? The (32 + 42) sieve generates a repeating pattern of the same pitch classes in each octave, all of which have the prime form (013569). While this is useful for demonstrating the mapping of a sieve onto pitch space, it doesn’t allow for much variation in the harmonic language of a piece. I have often felt that even when I limit myself a single pc set, (0124589) for instance, that having all 12 transpositions of that set still leaves me with a mostly open use of all pitches within the octave. One solution is to not think within the confines of pc sets, but to think within the confines of the octave. It is possible to create a sieve that is a combination of repeating interval series that do not have regular points of periodicity (i.e. they do not overlap at the same point within the octave). Each octave can be broken into its own pc set, but the pitch characteristics will change within each octave. This is created by using two or more residual classes with different factor/modulus values and different shift values. (Sidenote: I have found it is best to use at least 3 interval series to fill out the register and not produce lots of large intervals between adjacent pitches). Take the following example:

Using the range of the piano (0-87, where 0=A0)

60 + 91 + 77 = s

60 = [0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84]
75 = [5, 12, 17, 24, 31, 38, 45, 52, 59, 66, 73, 80, 87]
91 = [1, 10, 19, 28, 37, 46, 55, 64, 73, 82]
S = [0, 1, 5, 6, 10, 12, 17, 18, 19, 24, 28, 30, 31, 36, 37, 38, 42, 45, 46,
48, 52, 54, 55, 59, 60, 64, 66, 72, 73, 78, 80, 82, 84, 87]

And mapped onto pitch space (in which 0 represents A0, not C1) that would look like this:

The example above demonstrates three overlapping interval series mapped onto pitch space. However, because each interval series is shifted by a different amount the three series do not overlap at regular points, creating different pitch content for each octave, and variation in the sequence of pc sets. This artificial scale created through filtering by intervals can now serve as the basis for all pitch structure within a piece. Each octave has a unique set of pitches and contains a unique pc set. If you are a composer who is more inclined to use transpositions of a single pc set, the sieve above might become problematic considering each octave has a unique pc set, and therefore, different harmonic characteristics.

Another method of creating a sieve is to structure the interval series in a similar fashion as the sieves for major and minor scales above, but with a modulus value that is not 12. Take the following:

100 + 101 + 102 + 103 + 106 + 107 = [0,1,2,3,6,7,10,11,12,13,16,17,20,21,23,26,27…]

This method creates the same variation in pitch content per octave, but results in a concatenated series of the same pc set. The consistent modulus of 10 begins the series on a pitch class that is a minor 7th above the first pitch class in the previous series (e.g. if the first pc set begins on 9 (A), the next pc set will begin on 7 (G), the next on 5 (F) and so on). If we were to map this onto the range of the piano it would look like this:

This method of generating a sieve is beneficial for working with the same pc set, but not leaving yourself open to all transpositions mapped to the entire range of the keyboard. It is still up to the composer to develop a meaningful way to use these materials, but using a sieve as a jumping-off point can be very helpful in establishing a harmonic/pitch language that is atonal and has some of the freedom of “free atonality” using pitch sets and the unification of pc sets and subsets that can be gained from more structural approaches such as serial or 12-tone technique. Upon first learning about sieves I used them in a couple of pieces with relative success. More recently I find myself turning to sieves for generating pitch structures in all of my works. I have experimented with free atonality, serial techniques, stochastic pitch generation, Messiaen’s MOLT (you name it, I’ve probably tried it), but I find that sieves provide me with the perfect balance between a structured pitch/harmonic system and the freedom to choose how I want to order and organize those pitches linearly and vertically.

For more information on sieves, check out the following links.

You can also check out the chapter on sieves in Xenakis’ own Formalized Music

Keep an eye out for the next topic on sieves applied to rhythmic structures.

4 Comments

<<Previous

BY JON FIELDERMUSIC AND MENTAL HEALTH: HOW DIAGNOSING/TREATING MY MENTAL ILLNESS SAVED MY CREATIVITY

BY JON FIELDER
MUSIC AND MENTAL HEALTH: HOW DIAGNOSING/TREATING MY MENTAL ILLNESS SAVED MY CREATIVITY