Let's Talk Rhythm Part 1: Rationalizing the Irrational

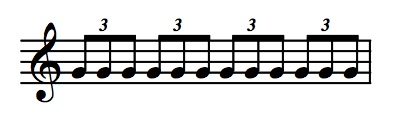
This post is the first of a series of three posts on the topic of rhythm, specifically complex rhythmic notation. The first segment (the one you're currently reading) will cover irrational meter, the second segment will focus on nested tuplets, and the last on generating rhythms through the use of sieves. My goal is to shed some light on these topics and (hopefully) clearly explain these more esoteric, complicated and sometimes overlooked rhythmic devices.

I chose to do irrational meter first because it’s something I’ve recently become very interested in.  Also, I had two separate conversations in one week recently (with two different people) on the topic of irrational meter, so it’s pretty fresh in my head right now. I don’t think it’s farfetched to say that many musicians never come into contact with irrational meters, and I personally have never heard the term “irrational meter” mentioned in a theory class (graduate and undergraduate). But, just because it isn’t a commonly used or understood rhythmic device doesn’t mean it isn’t a useful device. It’s like a rarely used, but sometimes necessary tool you keep in the bottom of a toolbox, just in case you need it one day, like a shingle froe.

So, what is irrational meter? In music, the term irrational does not have the same meaning as in mathematics with irrational numbers, which are real numbers that can’t be expressed as a ratio of integers, like Pi. In music, irrational is used to identify a meter in which the denominator is not a power of 2 (1, 2, 4, 8, 16...). Some examples of irrational denominators are 3, 7, 10, 12, 14, and these numbers represent fractions of a whole note - 1/3 of a whole note, 1/7, 1/10, etc. (more on that later). A measure notated with irrational meter uses standard rhythmic values, but the notes are played at a slightly faster or slower rate than normal (not irrational) meters. The example below shows 2 bars of music with the 2nd bar written in an irrational meter. We’ll dissect this later.

The point of an irrational meter is make a measure faster or slower in relation to the measures that come before and after. Another way to think about it would be to consider a measure with irrational meter as a very temporary change of tempo. But how is irrational meter created? The denominator of meter is derived by determining how notes fit into a whole note. Common divisions of a whole note are 2 half notes, 4 quarters, 16 sixteenths, etc. The same concept applies to irrational meters, but with different divisions of the whole. If a bar were broken into 6 equal divisions (also written as 2 quarter-note triplets) you could use 6 as a denominator. A measure using 6 as the denominator would be written as quarter-notes that move at the rate of a quarter-note triplet in a bar of 4|4. A bar could be broken into 12 equal divisions (eighth-note triplets), making the denominator 12. The numerator of an irrational meter represents the number of denominator divisions that are contained in the measure (4|4 containing 4 quarters, 6|8 containing 6 eighth notes, etc.).

So, let's break this down with some examples. To create a measure of 5|12 we first need to break a whole note in 12 equal divisions. This can represented as 4 beats of eighth-note triplets. Each note of the triplet is 1/12 of a whole note. If we were to excerpt 5 triplet-eighths of the total 12 and put them in a measure by themselves that would be a measure of 5|12, written as 5 eighth notes.

Each quarter broken into a group of 3 triplet 8ths

One measure of 5 8ths in which each 8th is played at the speed of a triplet 8th in the measure of 4|4

​These 8th notes are not played at the same rate as the eighth notes in a measure of 4|4, but at the rate of triplet eighth notes in a measure of 4|4. In this example, the measure of 5|12 moves at a faster rate, or tempo, than a measure of 4|4, because the eighth notes actually represent 1/12 of a whole note instead of 1/8 of a whole note. If the quarter-note tempo at 4|4 were 60 BPM, that would make the eighth note pulse 120 BPM in 4|4. In the measure of 5|12 the eighth note tempo would be 180 BPM, because a triplet eighth note is three times faster than a quarter note (60 x 2 = 120; 60 x 3 = 180).  The example below is the four measures in context.

Click the image to play an mp3 of the example

It’s a little more rare, but you can also use irrational meter to create a temporary slowing of the tempo. For example, the denominator 7 implies 7 equal divisions of a whole note. This is typically conceived as 7 quarter notes. However, it could theoretically also be written as a group of 7 eighth notes at a slightly slower rate than would fill the space of 8 eighth notes, like a group of 2 eighths in one beat of 6|8 measure. Granted, tuplets of a longer beat division (2:3, 7:8) are far more rare than tuplets of a shorter beat division (3:2, 5:4, etc.), but that doesn’t mean they aren’t possible. A measure of 8|7, with the 7 representing eighth notes at a slower rate, would be written as follows:

Click to play an mp3 of the example

A measure of 8|7 with the quarter-note pulse would look like this:

Yeah...you can click this one, too

This example causes a temporary slowing of the tempo, as opposed to a temporary quickening of the tempo with 5|12. However, when using 7 as a denominator for eighth notes it is a good idea to note in the score that the 7 represents the eighth note, as 7 is often a denominator used to represent quarter-notes. One way around this would be to put a metronome marking in the score. For instance, if the quarter-note tempo at 4|4 is 80 BPM, a measure of 8|7 with an eighth note pulse would have a tempo of eighth = 140 BPM. However, if the 7 denominator is a quarter-note pulse, then the quarter-note tempo would be 140 BPM, making the eighth-note tempo of the measure 280 BPM. This won’t have any impact on the aural result, but will effect the notation of the measure and how the performer interprets the it. If the goal is to make the measure seem slower than surrounding measure the eighth-note pulse should be used. If the goal is to make the measure move more quickly (almost 2x faster!) then the quarter-note 7 denominator should be used.

The examples above all show how irrational meter can be created, but what does it sound like in a more musical context? The example below contains an measure of irrational meter sandwiched between two measure of standard 5|4 and 4|4 meters. The measure is approached by a triplet and the first beat after the irrational meter is a beat of 4 sixteenth notes to help demonstrate the changing rhythmic rates in relation to the quarter-note meters.

Click it!

So there's a little crash course in irrational meter. One questions you might be asking yourself at this point is why would someone choose to do this? Doesn’t it make reading the score complicated for the performer? Isn’t there an easier way to notate these rhythms if they’re basically just tuplets? Why should a performer have to mathematically analyze the music just to play it? These are all great questions, and the short answer is that irrational meter achieves a certain rhythmic push and pull that is really not possible to notate any other way.


The whole point of using irrational meter is to use an irregular grouping of an uncommon fractional division of a beat. You wouldn’t use an irrational meter of 6|12 because that is 6 eighth-note triplets, which can be written more clearly in 2|4. However, 5|12 can only expressed as an irrational measure, because you can't divide a quarter-note into just 3 triplet eighths. That same 5|12 measure could be written as a measure of 5|8 with an 8th note tempo 3 times faster than the original quarter-note tempo, but I feel that would be just as confusing for a performer to read. Both options present problems, but only for sight reading purposes. I think it also goes without saying that music that uses irrational meter is not intended to be sight read perfectly (if at all). At the end of the day it is up to the composer to choose which method best communicates their idea to the performer in the cleanest notation possible. 


Tune in next week for a discussion on nested tuplets, how to break them down, how to create them and some thoughts on why a composer might use nested tuplets. 

Until next time!